引用: ゼロから作るDeep Learning ❹ ―強化学習編
-
価値を如何に定めるか?
- 状態 $s$と方策 $\pi$で決める→状態価値関数
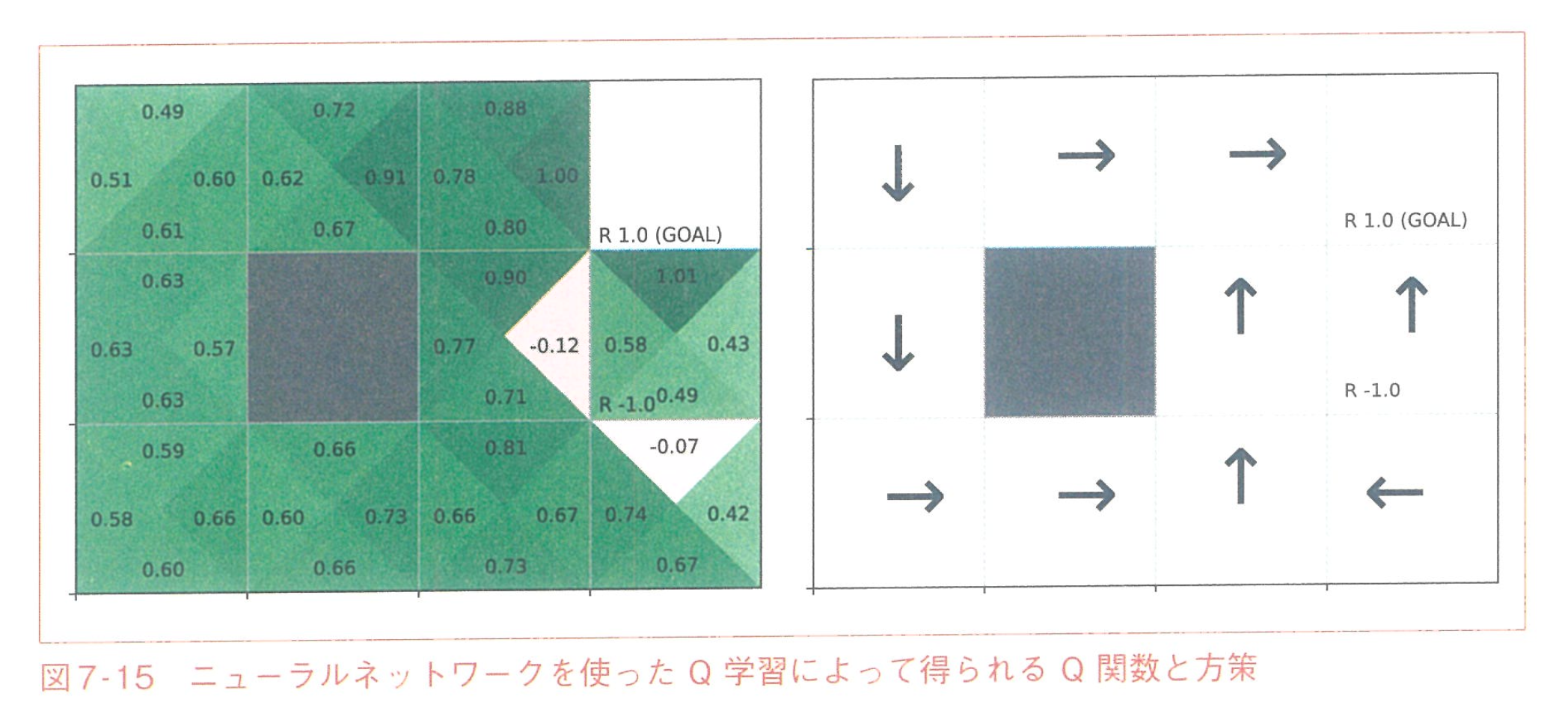
- 状態 $s$と方策 $\pi$と行動 $a$で決める→行動価値関数 (Q関数)
-
方策 $\pi$はグラフ遷移そのものと等しい存在
- 例えば, $\pi(a|s)$は状態 $s$から行動 $a$を実行する確率を表す
-
価値ベース手法
$$Q’(s_t,a_t) = Q(s_t,a_t) + \alpha(R_t + \gamma \max Q(s_{t+1},a)-Q(s_t,a_t))$$
- どうやって解くの?
- まず, 適当に[サンプリング](https://scrapbox.io/yuwd/%E3%82%B5%E3%83%B3%E3%83%97%E3%83%AA%E3%83%B3%E3%82%B0)してきた状態 $s$から $T$が最大となる $a, Q'$を探す
- 現在の $Q$と $Q'$の差を誤差と捉え, モデルを更新
- [DQN](https://yuiga.dev/blog/en/ja/posts/dqn//) では, これらに加えて「経験再生」と「ターゲットネットワーク」という概念が導入される
- 方策ベース手法
-
Q関数のように価値を近似するのではなく, 方策を直接近似する
-
REINFORCE / Actor-Critic (方策勾配法 → REINFORCE → Actor-Critic の順に勉強すると良い)
-
方策勾配法
- 方策 $\pi_{\theta}(a|s)$をNNで近似して, その勾配を求める
- 軌道 $\tau$が $\tau = {(s_0, a_0, r_0), ( s_1,a_1,r_1),…}$で与えられたとき
- 目的関数を次のように定義
$$J(\theta) = \mathrm{E}_{\tau_\theta}\lbrack G(\tau) \rbrack$$ - SGDと同様に勾配方向 $\nabla J(\theta)$にパラメタを更新する
$$\nabla J(\theta) = \mathrm{E}_{\tau_\theta} \lbrack \sum_t G(\tau) \nabla log \pi_\theta (A_t|S_t) \rbrack$$
-