- headはlossを小さく, tailはlossを大きくしたい
- 重み $w_i $を使ってlossを設計する (二値の場合)
$L_{EQL}=-\sum_{j=1}^{C}w_{j}log(\hat{p_{j}}),$ $w_{j}=1-E(r)T_{\lambda}(f_{j})(1-y_{j})$
In this equation, E(r) outputs 1 when r is a foreground region proposal and 0 when it belongs to background. And fj is the frequency of category j in the dataset, which is computed by the image number of the class j over the image number of the entire dataset. And Tλ(x) is a threshold function which outputs 1 when x < λ and 0 otherwise. λ is utilized to distinguish tail categories from all other categories and Tail Ratio (T R) is used as the criterion to set the value of it
- TRを元に $\lambda$ を決定する (Tail Ratio)
$TR(\lambda)=\frac{\sum_{j}^{C}T_{\lambda}(f_{j})N_{j}}{\sum_{j}^{C}N_{j}}$
- 多クラス問題の場合は,
$L_{SEQL}=-\sum_{j=1}^{C}y_{j}\log(\tilde{p_{j}})$, $\tilde{p_{j}}=\frac{e^{z_{j}}}{\sum_{k=1}^{C}\tilde{w_{k}}e^{z_{k}}}$
$\tilde{w_{k}}=1-\beta T_{\lambda}(f_{k})(1-y_{k})$
- でOK
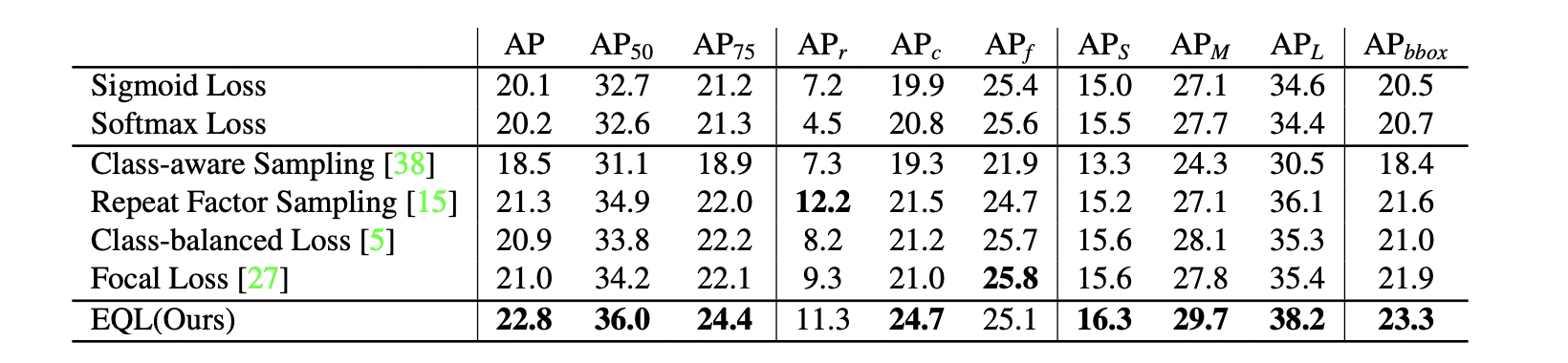
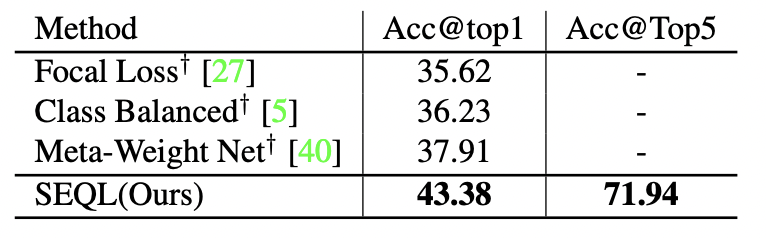
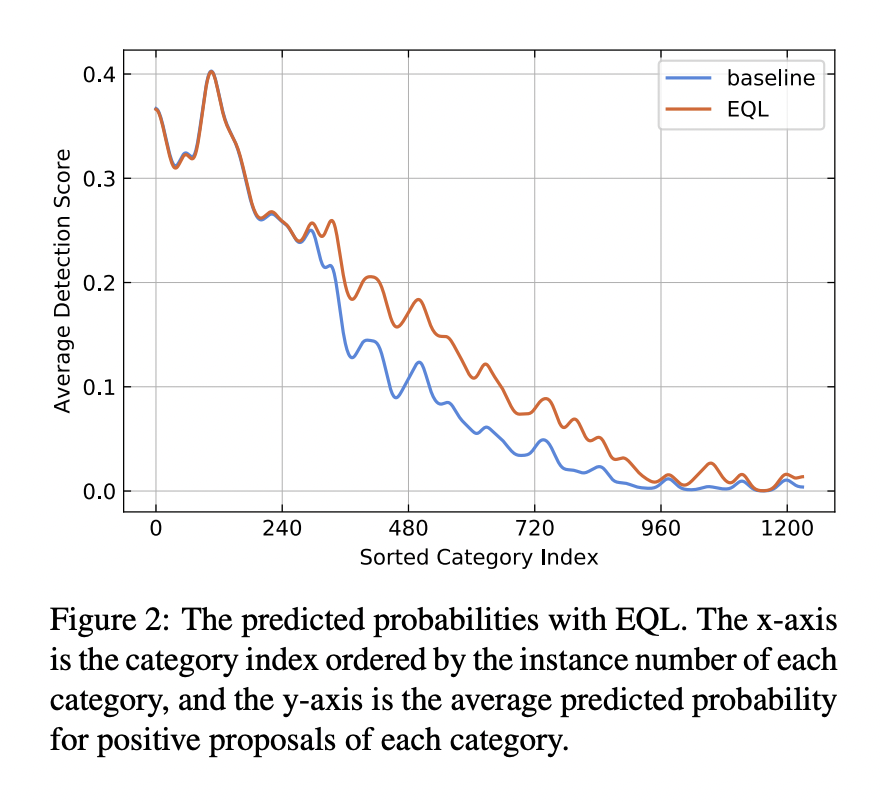
- 関連: Focal Loss