はじめに
- SAMの改良 (SAM : Sharpness-Aware Minimization)

Surrogate Gap Minimization Improves Sharpness-Aware Training
論文メモ
- 問題提起
-
SAMの計算式では, 本当にフラットな損失点を見つけているとは言えない
$$L_\mathcal{S}^\text{SAM}(\mathbf{w}) \triangleq \max_{|\mathbf{\epsilon}|_p\leq\rho} L_\mathcal{S}(\mathbf{w}+\mathbf{\epsilon})$$ -
例えば下の図では, 近傍 $f_p$について最適化すると, SAMの場合, 青に収束してしまう危険がある

-
本当に見るべきは以下に定義するsurrogate gap $h(x)$
$$h(x) := f_p(x) - f(x)$$ -
surrogate gap $h(x)$については, Hessianの最大固有値との間で以下の関係が成り立つことが証明できる
$$\sigma_{\mathrm{max}} ≈ \frac{2h(w_∗)}{ρ^2}$$- しかも, $O(ρ^3)$程度の誤差らしい
- Hessianの固有値とフラットさ
-
なので, surrogate gapがフラットな損失点へと収束することが理論的に証明されている
-
- 最適化の注意点
- 最適化したいのは, $f(x), f_p(x), h(x)$の三つ
- ただし, $min_w f_p(x) + \lambda h(x)$を最適化するのは少し注意が必要
- 例えば, $\nabla h = \nabla f_p - \nabla f$は $\nabla f$と $\nabla f_p$とで内積が負の値になることがある
- すなわち, 最適化のConflictが起きる可能性がある (下図参照)
- conflict = 片方を最適化すると片方が最適解から遠ざかる可能性がある
- なので, 実際のアルゴリズムは, $\nabla h$の直交成分を使って, 下図赤線の方向に解を更新する

-
SAMとの比較 (toy-setting)
- (GIFアニメなので自動でループ再生されてます)

- (GIFアニメなので自動でループ再生されてます)
-
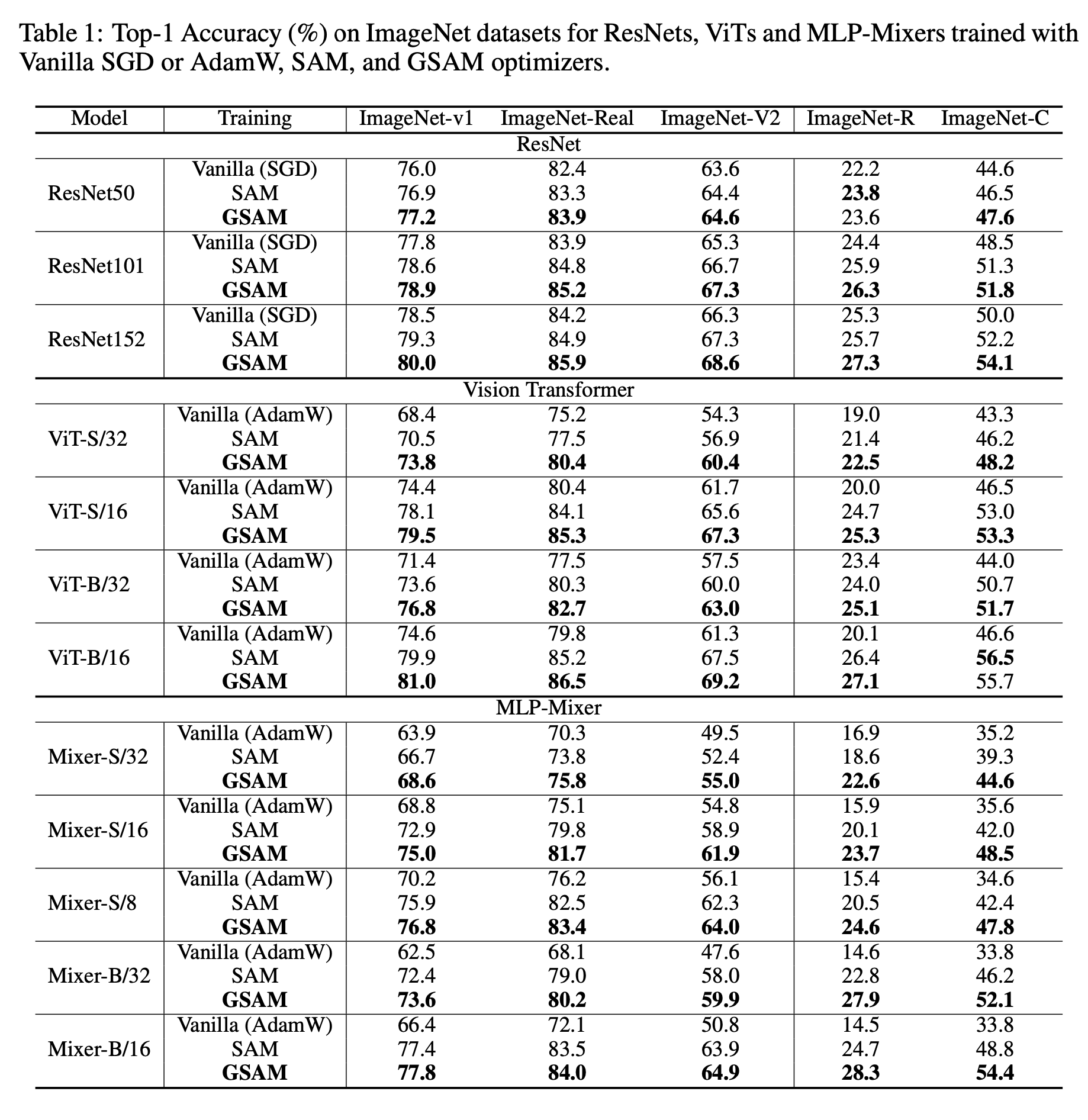
結果