1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
|
import sklearn.datasets
import torch
import numpy as np
np.random.seed(42)
torch.manual_seed(42)
X, y = sklearn.datasets.make_moons(200,noise=0.2)
import matplotlib.pyplot as plt
plt.scatter(X[:,0],X[:,1],s=40,c=y,cmap=plt.cm.binary)
X = torch.from_numpy(X).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self, activate="relu"):
super(Net,self).__init__()
h = 6
self.fc1 = nn.Linear(2,h)
self.fc2 = nn.Linear(h,2)
self.relu = nn.ReLU()
self.tanh = F.tanh
self.activate = activate
def forward(self,x):
x = self.fc1(x)
x = self.relu(x) if self.activate == "relu" else self.tanh(x)
x = self.fc2(x)
return x
def predict(self,x):
pred = F.softmax(self.forward(x))
ans = []
for t in pred:
if t[0]>t[1]:
ans.append(0)
else:
ans.append(1)
return torch.tensor(ans)
#Initialize the model
model = Net()
#Define loss criterion
criterion = nn.CrossEntropyLoss()
#Define the optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
#Number of epochs
epochs = 50000
#List to store losses
losses = []
for i in range(epochs):
#Precit the output for Given input
y_pred = model.forward(X)
#Compute Cross entropy loss
loss = criterion(y_pred,y)
#Add loss to the list
losses.append(loss.item())
#Clear the previous gradients
optimizer.zero_grad()
#Compute gradients
loss.backward()
#Adjust weights
optimizer.step()
from sklearn.metrics import accuracy_score
print(accuracy_score(model.predict(X),y))
def predict(x):
x = torch.from_numpy(x).type(torch.FloatTensor)
ans = model.predict(x)
return ans.numpy()
# Helper function to plot a decision boundary.
# If you don't fully understand this function don't worry, it just generates the contour plot below.
def plot_decision_boundary(pred_func,X,y):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx,yy=np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
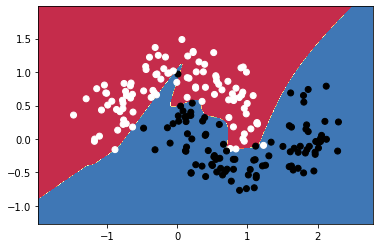
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.binary)
plot_decision_boundary(lambda x : predict(x) ,X.numpy(), y.numpy())
|