-
グラフをそのままTransformerにブチこむ手法
-
入力について
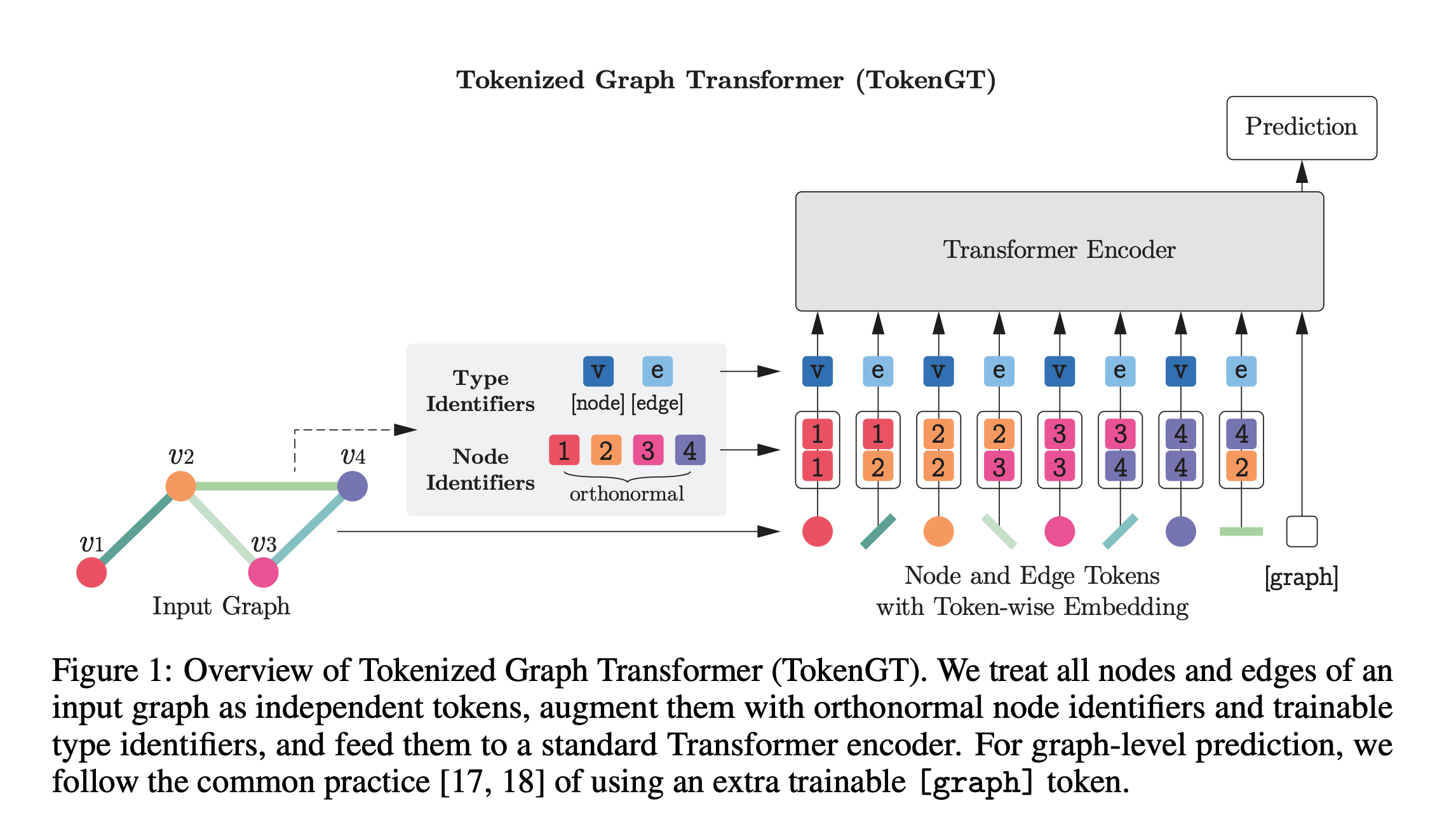
- まず, ノードとエッジをそれぞれ独立なものとして捉え, それぞれを同等にトークン $X$とする
- そのトークンに, ノードなのかエッジなのかを判別するType Identifiersをconcatして入力
-
トークン $X$について
- トークンには直交行列 $P$を用いる
- なんで直交?→後述
- ノード $v \in \mathcal{V}$については, $X \leftarrow \lbrack X_u, P_v, P_v\rbrack$
- エッジ $(u,v) \in \mathcal{E}$については, $X \leftarrow \lbrack X_{(u,v)}, P_u, P_v\rbrack$
- こうすれば, Attentionの内積計算でe=1, 0 (繋がり)を表現でき, グラフ構造を扱える
- 例えば
- ノード $k \in \mathcal{V}$がエッジ $e := (u,v) \in \mathcal{E}$につながってるなら
- $[P_u,P_v\rbrack [P_k,P_k\rbrack ^\top = 1$になるし, そうでないなら0になる
- ( $\because k = u $or $k = v$で $P$は直交行列)
- トークンには直交行列 $P$を用いる
-
直交行列 $P$について→どうやって $P$を得るの?
- 方法は2つ提案されている
- 1つ目: ORF (Orthogonal Random Features)
- 2つ目: ラプラシアン行列の固有ベクトルを用いる (固有値分解)
- ラプラシアン行列の固有ベクトルはグラフにおけるPositional Encodingとある種同等なので, モデルにとっては有益
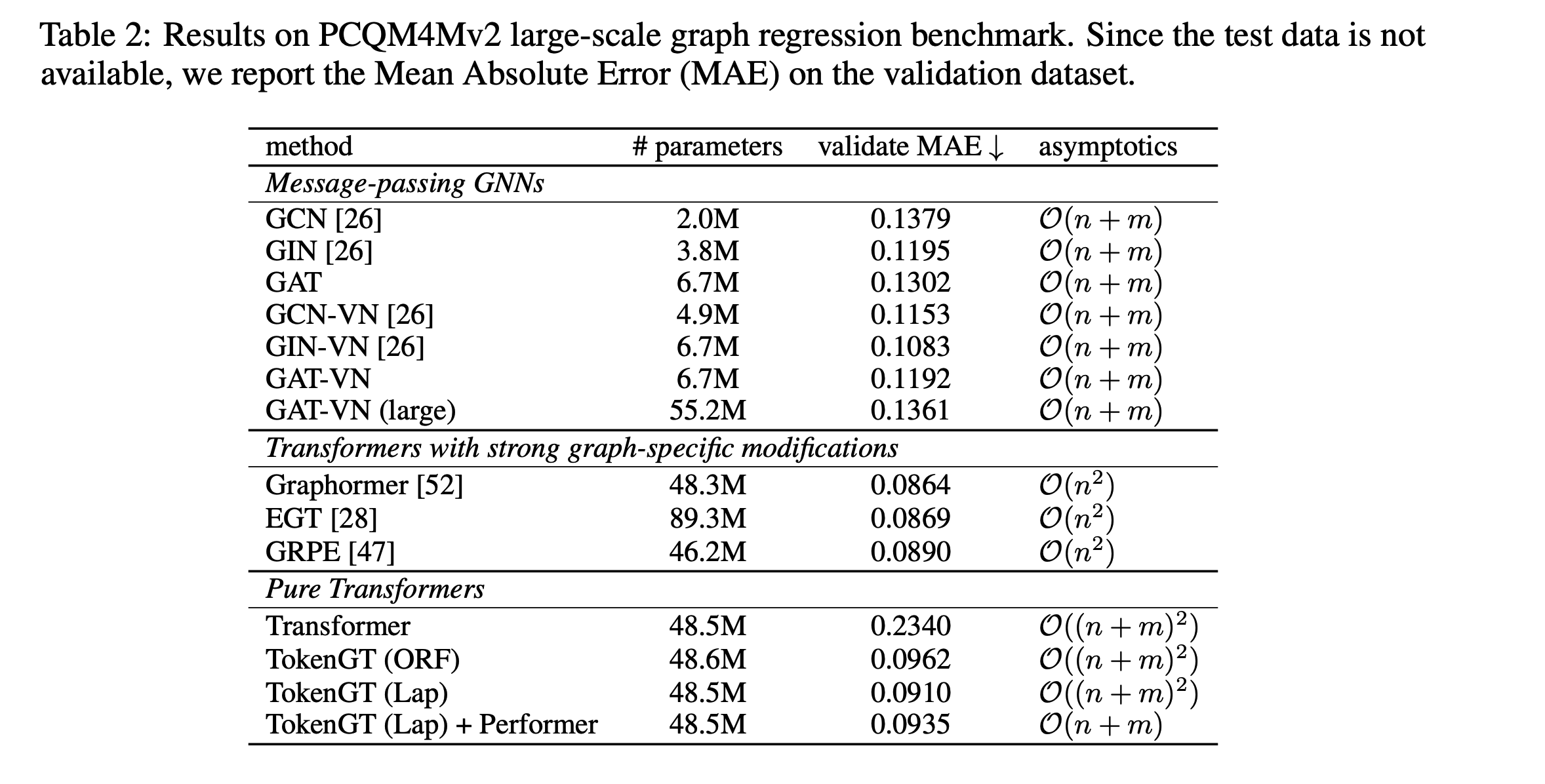
- ORFより良い精度が出たらしい
-
このあたりのデータセットの知見ないから結果みても何ともいえんな…