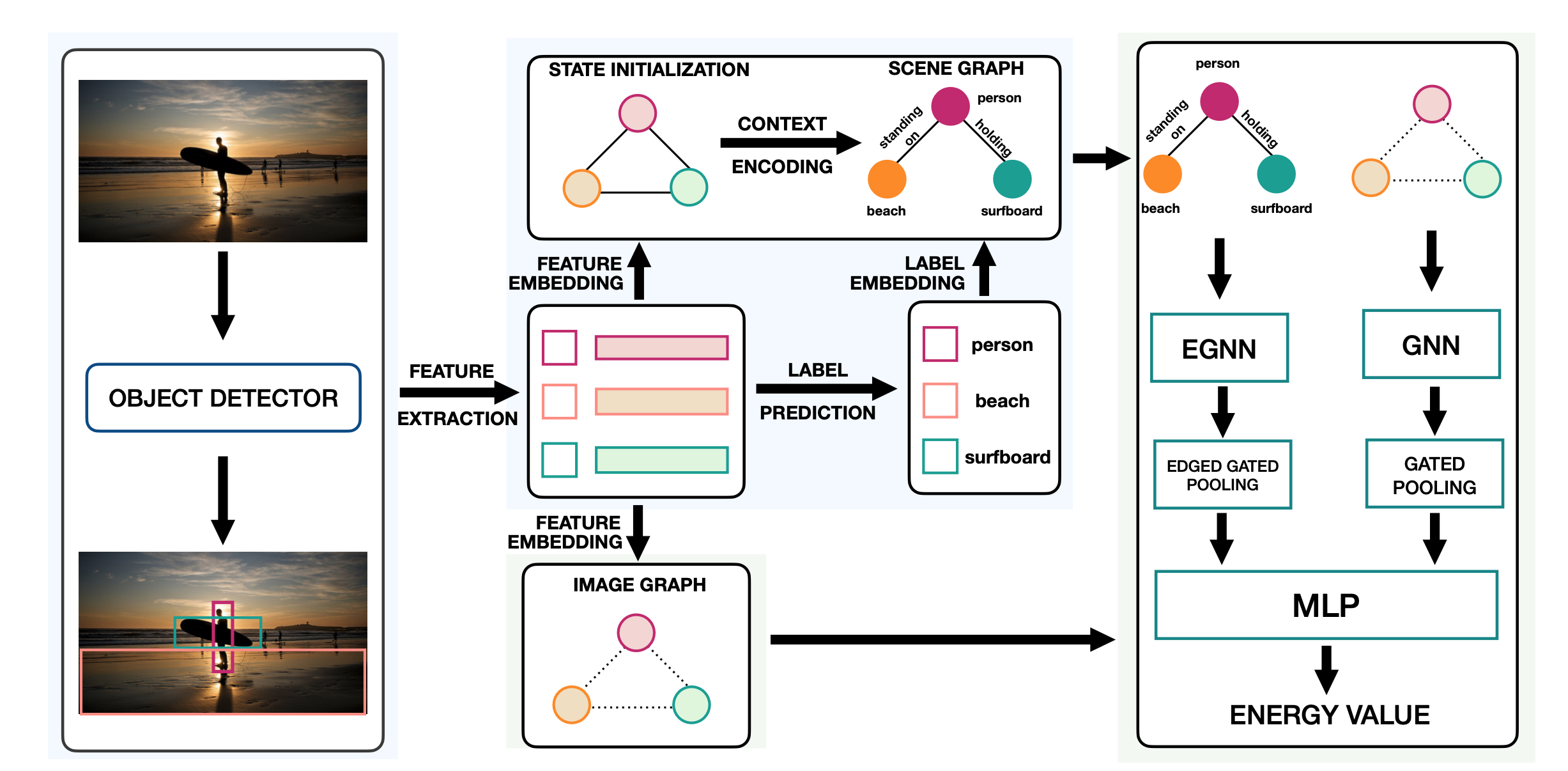
【相関係数】Pearson・Spearman・Kendallの使い分け
· ☕ 1 min read
ピアソン $$ r_{xy} = \frac{{\displaystyle \sum_{i = 1}^n (x_i - \overline{x}) (y_i - \overline{y})}}{\sqrt{{\displaystyle \sum_{i = 1}^n (x_i - \overline{x})^2}} \sqrt{{\displaystyle \sum_{i = 1}^n (y_i - \overline{y})^2}}} = \frac{s_{xy}}{s_xs_y} $$ データ(X,Y)が連続で正規分布に従っていることが前提 なので外れ値に弱い スピアマン $$ \rho_{xy} = \frac{\sum_{i=1}^{n}(R(x_i) - \overline{R(x)})(R(y_i) - \overline{R(y)})} {\sqrt{\sum_{i=1}^{n}(R(x_i) - \overline{R(x)})^{2}\cdot\sum_{i=1}^{n}(R(y_i)-\overline{R(y)})^{2}}} = 1 - \frac{6\sum_{i=1}^{n}(R(x_i) - R(y_i))^{2}}{n(n^{2} - 1)} $$ $R(x)$は $x$の順位 順位をそのままピアソンの式に当てはめるイメージ 正規分布・連続という仮定がない分使い勝手が良い ケンドール $$ \tau_{xy} ...