-
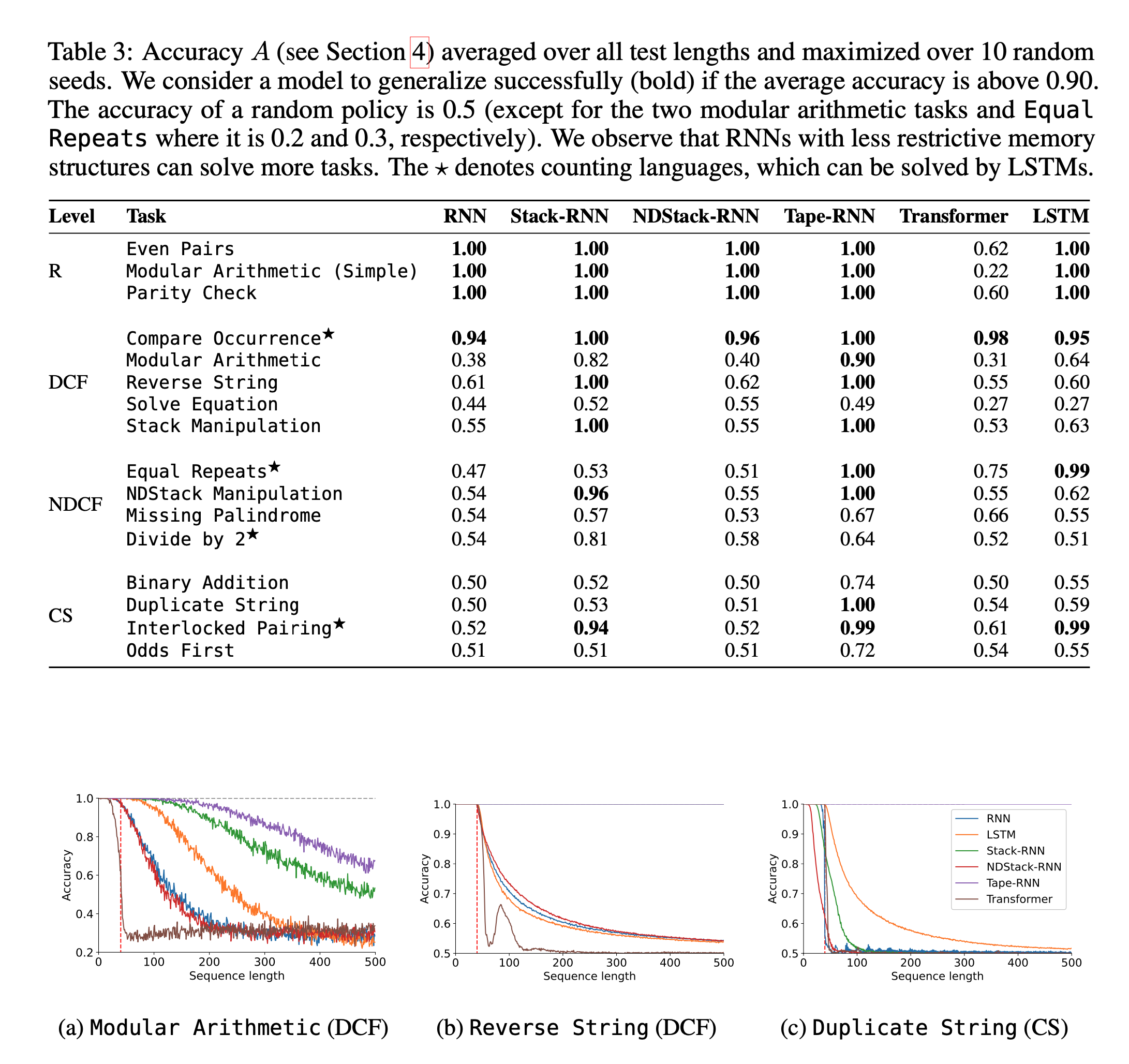
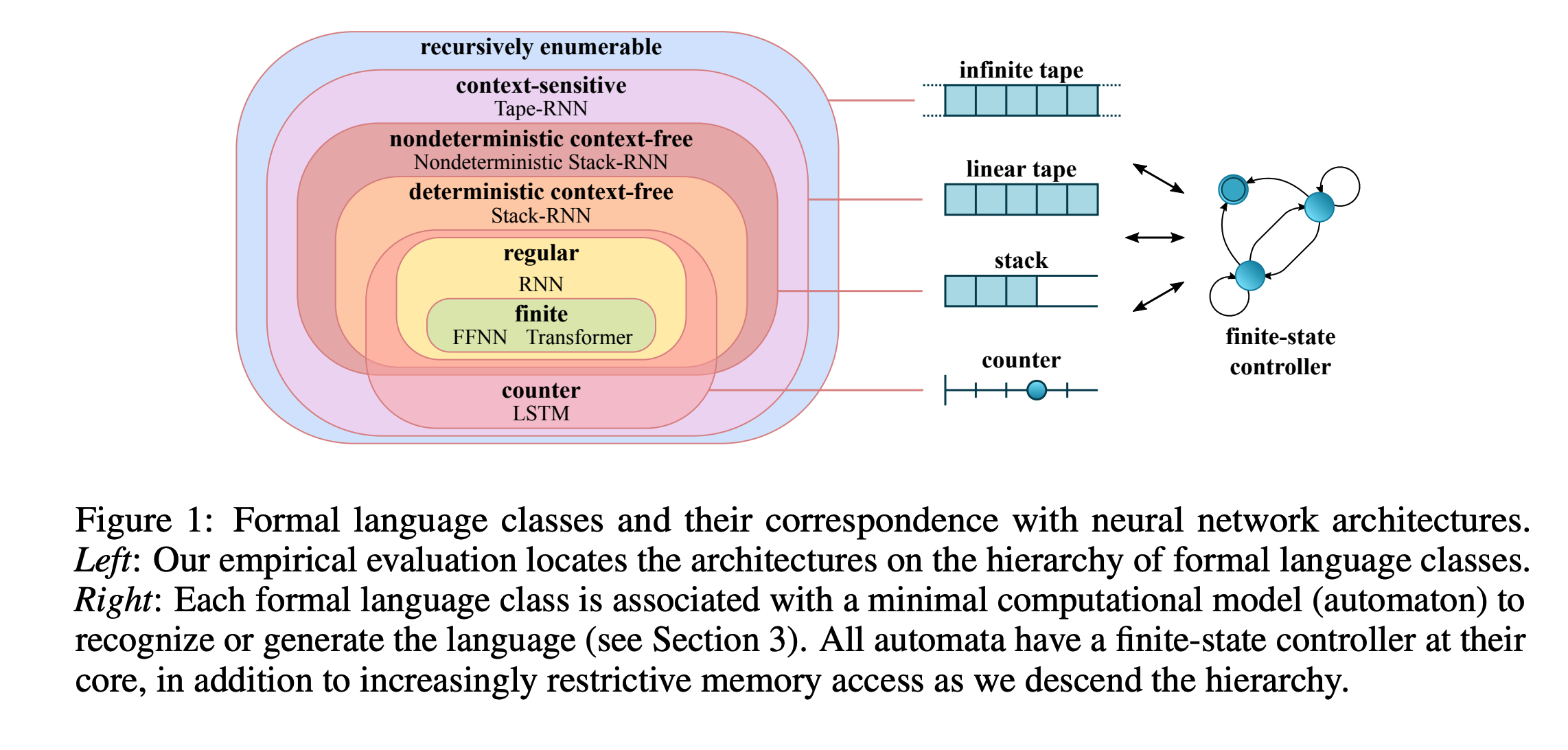
Chomsky Hierarchyにおいて, 各モデルがどのクラスに属するかを実験的に示した
- 各階層はオートマトンの性質と紐付いている
- RNNやTransformerは無限ステップにおいてチューリング完全であることが理論的に証明されているが, 有限ステップにおいて各モデルがどのクラスに属するかの研究は未だ発展中
- 例えば, Transformerがある種の正則言語を識別できないことが理論的に証明されたり.
- RNNとチューリング完全性
-
問題設定
- アルファベット $\Sigma$のone-hotベクトルのトークン列 $z_1,z_2,…,z_k$について
- 前半 $[1,l \rbrack$をinputとし, 後半 $(l,k\rbrack$を予測する
-
モデル
- Transformer
- RNN
- LSTM
- Stack-RNN
- push, popのみできるスタックを保持
- NDSTack-RNN
- 非決定性のスタックを保持
- 動的計画法を用いてシミュレート(?)
- Tape-RNN
- チューリングマシン自体に則り, 有限ではあるがテープを持つRNN
-
言語タイプ
- R→正則言語
- CF→文脈自由
- CS→文脈依存
- RE→ 回帰的列挙 Recursively enumerable
-
言語タイプによって要請されるオートマトンの種類は異なる
- R→FSAでOK
- CF→Push-down (PDA)
- CS → Linear bounded automaton (LBA)
- 初めて聞いた
- 線形拘束オートマトン
- https://ja.wikipedia.org/wiki/線形拘束オートマトン
- テープが有限長に拘束されてるだけらしい
- 初めて聞いた
- RE → Turing Machine
-
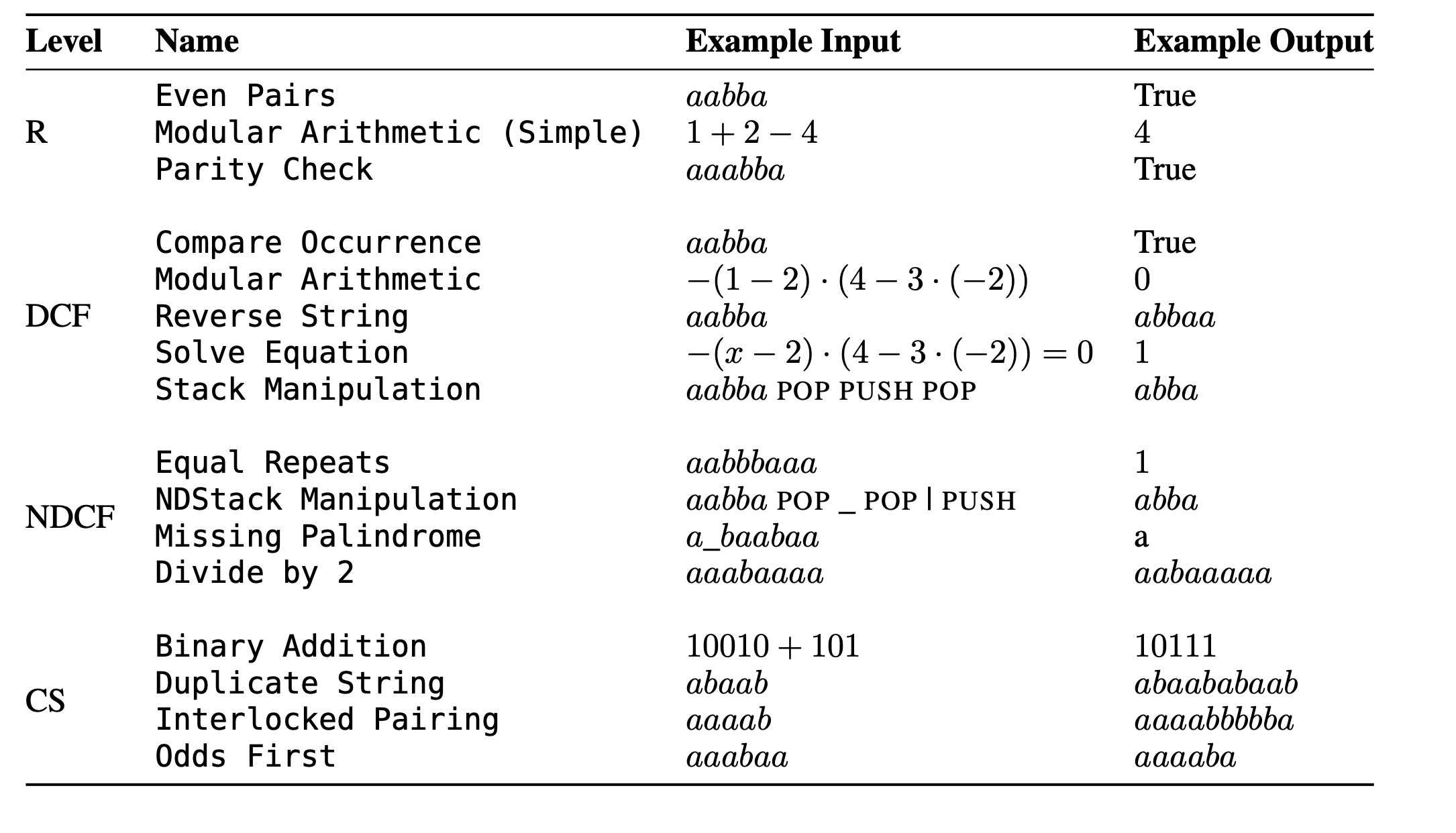
タスク
- Even Pairs(R)
- 2進数列、例えばx = aabbaが与えられたとき、absとbasの数が偶数かどうか計算しなさい。aabbaの場合、abとbaが1つずつなので、合計数は2であり、偶数、すなわち、y=bとなる(ここで、奇数をa、偶数をbと任意に同一視している)
- Modular ARrithmetic(Simple)(R)
- {0, 1, 2, 3, 4}の数列と{+, -, -}の演算が与えられたとき、その結果を5のモジュロで計算せよ。例えば、x = 1 + 2 - 4 は y = 4 と評価される
- Parity Check (R)
- 2進文字列、例えば aaabba が与えられたとき、bs の数が偶数であるかどうか計算しなさい。x = aaabbaの列は2個のbsを含み、これは偶数、すなわちy = bである(ここで、奇数をa、偶数をbと任意に同一視する。 発生比較 (DCF) 2進文字列が与えられたとき、asの数がbsの数より大きいかどうかをチェックする。例えば、x = aabbaは3つのasと2つのbsを含み、つまりasの方が多いのでy = aとなる。
- Modulear Arithmetic(DCF)
- {0, 1, 2, 3, 4}の数列、括弧、{+, -, -}の演算が与えられたら、5のモジュロの結果を計算しなさい。たとえば、x = -(1-2)-(4-3-(-2)) という数列は、y = 0 と評価されます。
- Reverse String (DCF)
- x = aabba などの 2 進文字列がある場合、その逆、すなわち y = abbaa を計算します。
- Solve Equation(DCF)
- {0, 1, 2, 3, 4}の数、括弧、{+, -, -}の演算、および未知の変数xからなる方程式がある場合、方程式が5モジュロで成り立つようなxの値を計算する。例えば、x = -(x -2) - (4 - 3 - (-2)) = 0 modulo 5 は、x = 1、すなわち y = 1 で成立する
- Stack Manipulation(DCF)
- スタックの内容を表す 2 進文字列と PUSH または POP 操作のシーケンスが与えられたとき、スタック上の操作を実行し、最終的なスタックの内容を返す。例えば、スタック aabba に対して POP PUSH POP シーケンスを実行すると、すなわち x = aabba POP PUSH POP とすると、スタック y = abba になる。等しい繰り返し (NDCF) n = m, m = l, n = l のいずれかの al bm an の形のシーケンスがあるとき、l = m (ケース 0), m = n (ケース 1), n = l (ケース 2) のいずれかを分類しなさい。例えば、x = aabbbaaaの場合、m = nとなり、結果はy = 1となる。
- NDStack Manipulation (NDCF)
- Stack Manipulationタスクと同様に、スタックの内容を表す2進文字列と、PUSHとPOPアクションのシーケンスが与えられる。しかし、アクションの1つは空のトークンに置き換えられ、入力シーケンスの最後にのみ提供される。出力は、省略されたアクションを正しい位置に置いて、すべての操作を実行した後のスタックである。例えば、スタック aabba とアクション POP _ POP | PUSH のシーケンス、すなわち x = aabba POP _ POP | PUSH について、 _ は省略されたアクションの位置(すなわち PUSH)を示し、 | はアクションシーケンスの終わりを示す、結果のスタックは y = abba である。
- Missing Palindrome(NDCF)
- 1つのトークンが省略された2進回文、例えばx = a_baabaaが与えられたとき、その値、すなわちy = a(aabaabaaを得るために)を推論しなさい。
- Divide by 2(NDCF)
- a(n-1) b am という形の文字列が与えられたとき、 aceil(n/2) b afloor(n/2)+m という形の文字列を出力しなさい。例えば、x = aaabaaaa に対応する出力は y = aabaaaaa となる。
- Binary Addition (CS)
- 2 つの二進数、例えば 10010 と 101 が与えられたとき、その和を底 2 で計算しなさい、すなわち x = 10010 + 101 に対して y = 10111 と計算しなさい。
- Duplicate String (CS)
- 2進文字列、例えば x = abaab が与えられたとき、その文字列を2回、すなわち y = abaababaab と出力しなさい。
- Even Pairs(R)