はじめに

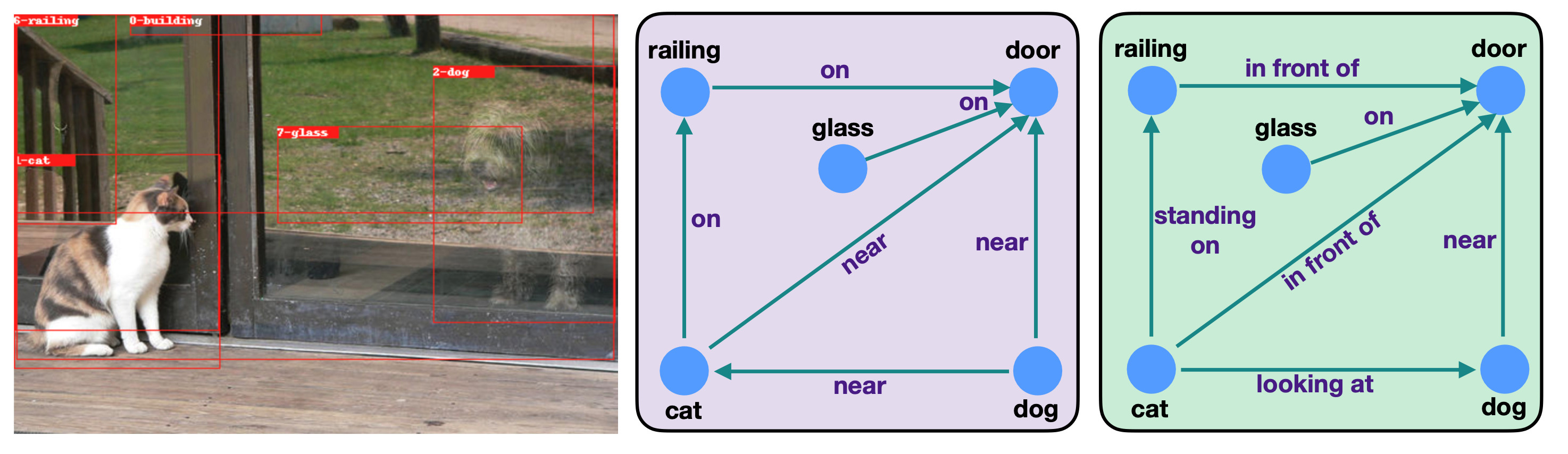
• Energy Based Modelを用いて画像からscene graphを生成する手法(フレームワーク)を提案
  • 既存手法は次のようにクロスエントロピーでscene graphを生成する
    $$\log p(SG|I)=\sum _{i\in O}\log p(o_i|I)+\sum _{j\in R}\log p(r_j|I).$$
  • このとき, object $O$とrelation $R$が互いに独立に計算されている
    • ここが問題で, 本来なら互いに弱い依存性があるはず
    • したがって, データがある確率分布 $p_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})$からサンプリングされていると仮定し, Energy Based Modelに基づいてエネルギー関数 $E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})$を定義し, lossを設計

• スライド

Energy-Based Learning for Scene Graph Generation

前提知識

• Energy Based Modelについては以下を見てくだはれ.

• Stochastic Gradient Langevin Dynamicsについては以下を見てくだはれ.

解説

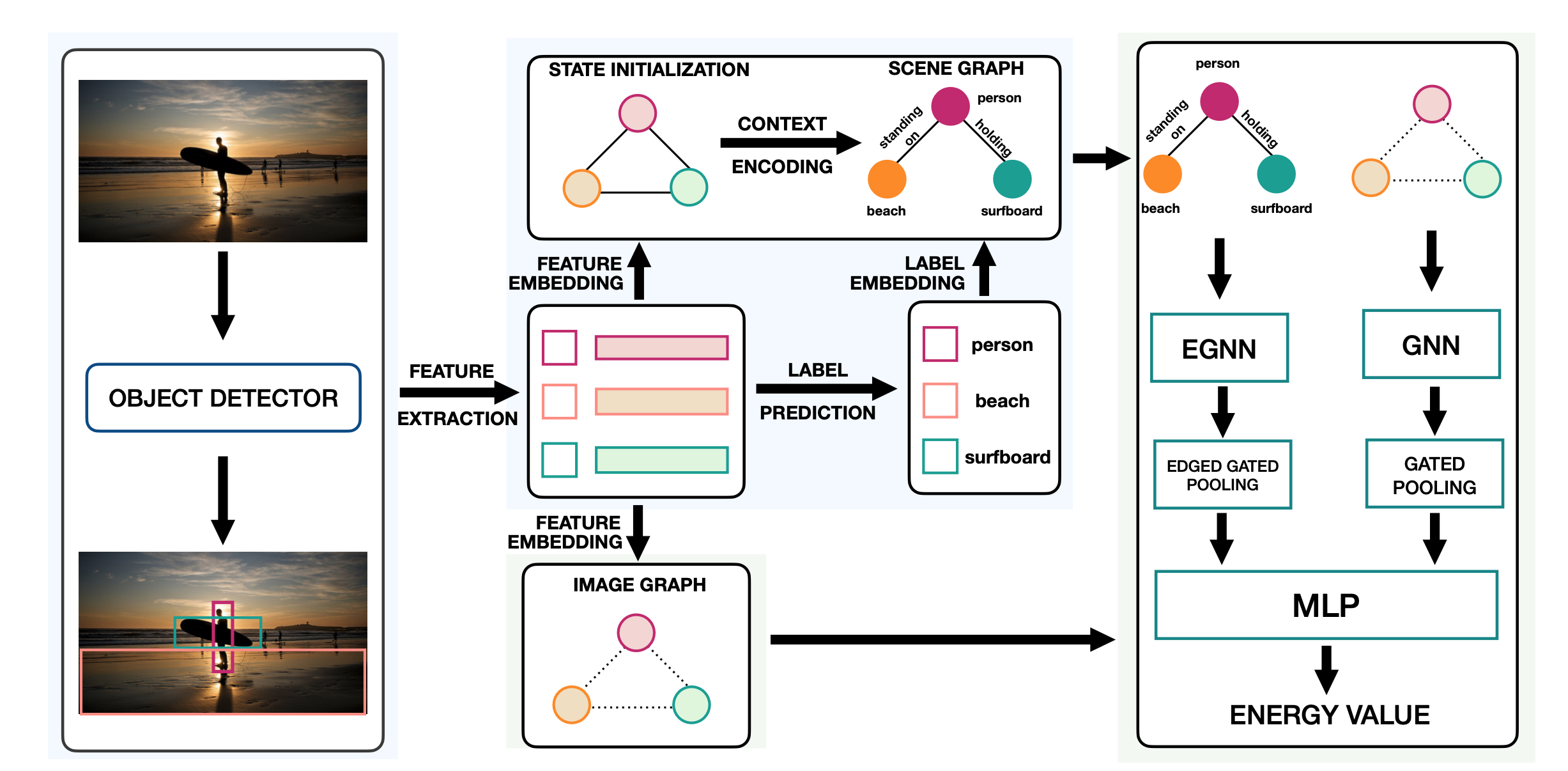
• 流れ

  • Faster-RCNNで物体検出
  • 各領域をノードとして, Image Graphを ${\mathsf{G}}_{\mathcal{I}}$,Scene Graph を ${\mathsf{G}}_{\mathcal{SG}}$とする
  • エネルギー関数 $E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})$は以下のようにGNNとEGNN(後述)を通した後に, pooling→concatしてMLPに通したものとする
    $$E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})=\mathrm{MLP}[f(\mathrm{EGNN}({\mathrm{G}}_{SG}));g(\mathrm{GNN}({\mathsf{G}}_{\mathcal{I}}))]$$
  • エネルギー関数 $E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})$について, 以下のようにlossを定義
    $${\mathcal{L}}_{total}={\lambda }_e{\mathcal{L}}_e+{\lambda }_r{\mathcal{L}}_r+{\lambda }_t{\mathcal{L}}_t,$$

• lossについて

  • ${\mathcal{L}}_e$について, GTのグラフを $G^{+}$として以下のように定義
    $${\mathcal{L}}_e=E_{\theta }({\mathsf{G}}_{\mathcal{I}}^{+},{\mathsf{G}}_{SG}^{+})-\underset{{\mathsf{G}}_{SG}\in SG}{min}{E}_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}).$$

  • この式の意味するところは次の通り

    • 元の確率分布 $p_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})$を
      $$p_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})=\frac{\text{exp}(-E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}))}{Z_{\theta }}=\frac{\text{exp}(f_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}))}{Z_{\theta }}$$
    • とすると,

$${\mathcal{L}}_e=-f_{\theta }({\mathsf{G}}_{\mathcal{I}}^{+},{\mathsf{G}}_{SG}^{+})+\underset{{\mathsf{G}}_{SG}\in SG}{max}{f}_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}).$$

• となり, このlossの最適化(loss↓)は $f_{\theta }({\mathsf{G}}_{\mathcal{I}}^{+},{\mathsf{G}}_{SG}^{+})$を最大化(↑)して, サンプリングしてきた $f_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})$を最小化するので, trainの値を引き上げ, sampleの値を引き下げることになる
• 第二項の計算はサンプリングが必要なので, Stochastic Gradient Langevin Dynamicsによってサンプリング
  $${\mathbf{O}}^{\tau +1}={\mathbf{O}}^{\tau }-\frac{\lambda }{2}{\mathrm{\nabla }}_{\mathbf{O}}{E}_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}^{\tau })+{ϵ}^{\tau }$$
  $${\mathbf{R}}^{\tau +1}={\mathbf{R}}^{\tau }-\frac{\lambda }{2}{\mathrm{\nabla }}_{\mathbf{R}}{E}_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}^{\tau })+{ϵ}^{\tau }$$

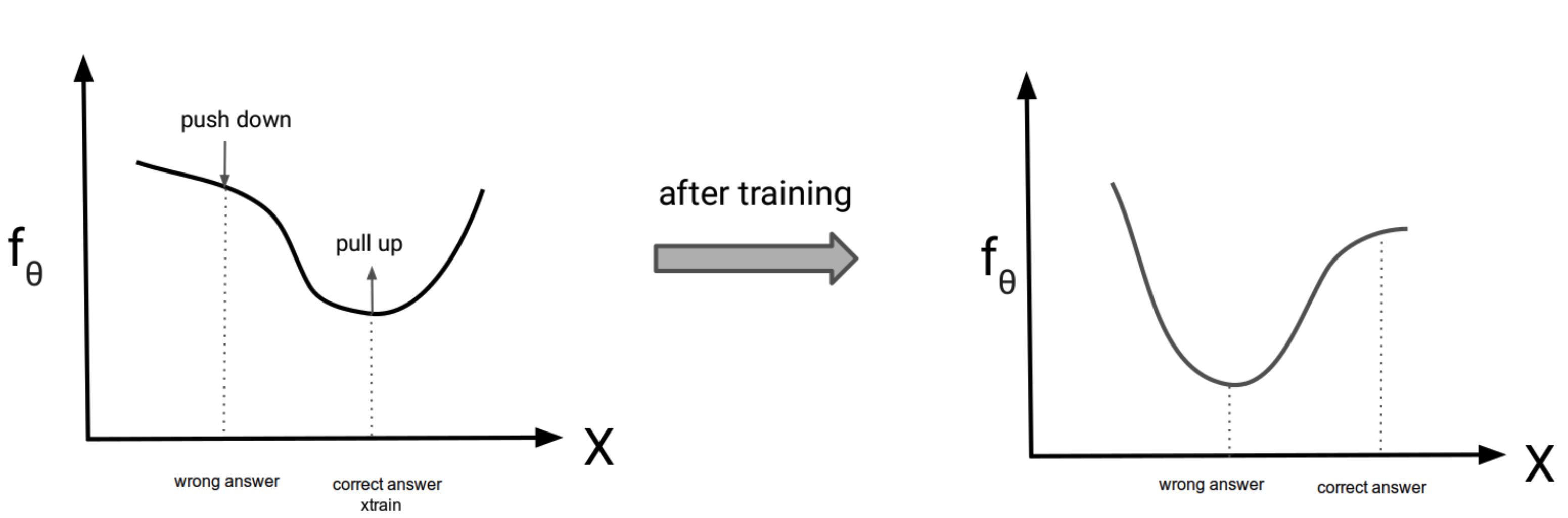
引用: https://deepgenerativemodels.github.io/assets/slides/cs236_lecture11.pdf

• ${\mathcal{L}}_r$について
  - ${\mathcal{L}}_e$だけだと解が爆発してしまったので(そらそうだろ), 正則化項としてのloss ${\mathcal{L}}_r$を追加
  $${\mathcal{L}}_r=E_{\theta }({\mathsf{G}}_{\mathcal{I}}^{+},{\mathsf{G}}_{SG}^{+}{)}^2+E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG}{)}^2.$$

• エネルギー関数について

  • 以下のように定義
    $$E_{\theta }({\mathsf{G}}_{\mathcal{I}},{\mathsf{G}}_{SG})=\mathrm{MLP}[f(\mathrm{EGNN}({\mathrm{G}}_{SG}));g(\mathrm{GNN}({\mathsf{G}}_{\mathcal{I}}))]$$
  • GNNはGated Graph Neural Networks (GG-NNs)を使用
  • EGNNは新たに提案された手法

• EGNN (Edge Graph Neural Network) について

  • ノードにおけるmessage ${\mathbf{m}}_i^t$を以下のように定義
    $${\mathbf{m}}_i^t=\alpha \underset{\text{node to node message}}{\underbrace{{\mathbf{W}}_{nn}\left(\sum _{j\in {\mathcal{N}}_i}{\mathbf{n}}_j^{t-1}\right)}}+(1-\alpha )\underset{\text{edge to node message}}{\underbrace{{\mathbf{W}}_{en}\left(\sum _{j\in {\mathcal{N}}_i}{\mathbf{e}}_{j\to i}^{t-1}\right)}}$$

  • エッジにおけるmessage ${\mathbf{d}}_{i\to j}^t$を以下のように定義
    $${\mathbf{d}}_{i\to j}^t={\mathbf{W}}_{ee}[{\mathbf{n}}_i^{t-1}\Vert {\mathbf{n}}_j^{t-1}]$$

  • それぞれがMessage-Passing方式でGRUに通される

    • GRU (ゲート付き回帰ユニット)

• 定量的結果 (VGTree + Energey-Based Loss)
  

  

  
  
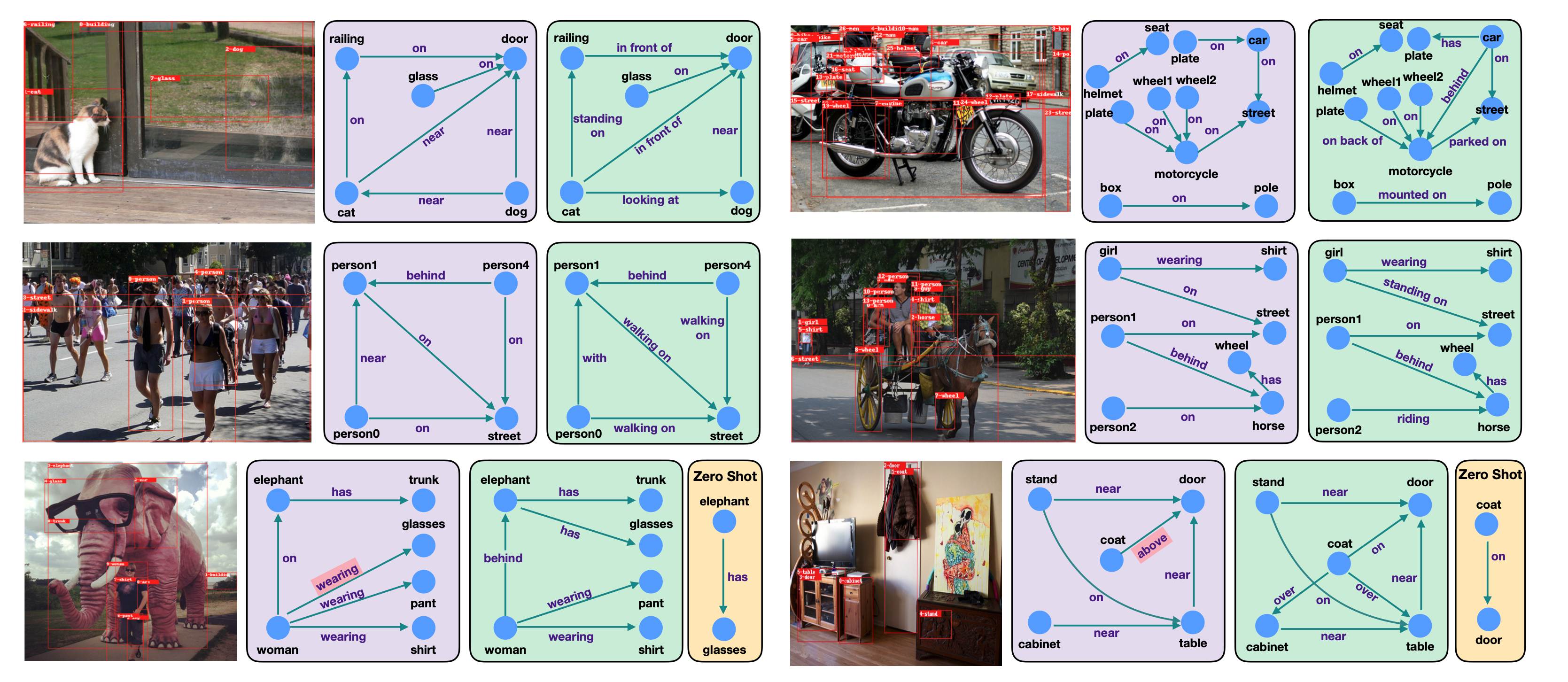
  • 一番上の左の結果
    • <cat, near, door> → <cat, in front of, door>
    • <dog, near, cat> → <cat, looking at, dog>
    • となっており, よりinteractiveなrelationが張られている