• Energy Based Model

  • 生成モデルによく用いられる
    • 拡散モデルとも関係が深い
    • 分類回帰問題についてはYour classifier is secretly an energy based model and you should treat it like oneを参照
  • GANやVAE同様, データ $x$は何らかの高次元確率分布 $p(x)$からサンプリングされたものと仮定する

• EBMでは以下のように確率分布 $p(x)$を仮定し, $E_{\theta}(\boldsymbol{x})$をエネルギー関数, $Z_{\theta}$を分配関数と呼ぶ
  $$p_{\theta}(\boldsymbol{x}) = \frac{\textrm{exp}(-E_{\theta}(\boldsymbol{x}))}{Z_{\theta}}$$

• $Z_{\theta}$はただの正規化係数で以下の通り.
  $$Z_{\theta} = \int_{x} \textrm{exp}(-E_{\theta}(\boldsymbol{x}))d\boldsymbol{x}$$

• EBMのお気持ち

  • $Z_{\theta}$さえ度外視してしまえば, 正規化という確率分布の大原則から逃れられるため, $E_{\theta}(\boldsymbol{x})$をNNでどのようにでも近似してよいことになり嬉しい

  • でも $Z_{\theta}$無視できないよね

  • → $Z_{\theta}$を直接計算するのは困難なのでサンプリングしましょう

    • 方法1. MCMC
      • 制限ボルツマンマシン時代はGibbs SamplingのようなMCMCが主流であった
      • 高次元空間でのMCMCは非常に品質が悪く, 速度も遅いため, NNにより高次元なベクトルを扱う今日では単純なMCMCは扱われない
    • 方法2. Stochastic Gradient Langevin Dynamics
      • したがって近年ではMCMCにLangevin Dynamicsを組み込んだSGLDを使うことが多い

  • また, EBMでの最適化は単なる対数尤度最大化

    • 負の対数尤度 $-log{p_{\theta}(\boldsymbol{x})}$の勾配を計算していくと

$$
\begin{align} -\nabla_{\theta}log{\frac{\textrm{exp}(-E_{\theta}(\boldsymbol{x}))}{Z_{\theta}}} &= \nabla_{\theta}E_{\theta}(x_{train}) + \nabla_{\theta}\textrm{log}Z_{\theta} \\
&= \nabla_{\theta}E_{\theta}(x_{train}) + \frac{1}{Z_{\theta}}\int \nabla_{\theta}\textrm{exp}(-E_{\theta}(x))dx \\
&= \nabla_{\theta}E_{\theta}(x_{train}) - \int \frac{\textrm{exp}(-E_{\theta}(x))}{Z_{\theta}}\nabla_{\theta}E_{\theta}(x)dx \\
&= \nabla_{\theta}E_{\theta}(x_{train}) - \mathbb{E}_{sample}[\nabla_{\theta}E_{\theta}(x_{sample})\rbrack
\end{align}
$$

• 上のようになり, trainの勾配とsampleの勾配の差の方向に解を更新していけば良い

• 後は勾配さえ計算できればよく, 第二項のサンプリングにMCMCの一種であるStochastic Gradient Langevin Dynamicsを使うだけ

• EBMにおける最適化のイメージ

  • $p_{\theta}(\boldsymbol{x}) = \frac{\textrm{exp}(f_\theta(x_{train}))}{Z_{\theta}}$を最大化したい
  • ということは, $f_\theta(x_{train})$を無限にでかくすれば良い
  • だが, 周辺化された $Z_{\theta}$は小さくなる方向に働くので, サンプル点 $x_{train}$以外の点の値は小さくなる
  • つまり, trainデータの値が押し上げられ, sampleの値を押し下げられることになる (下図)
    

    

    
    

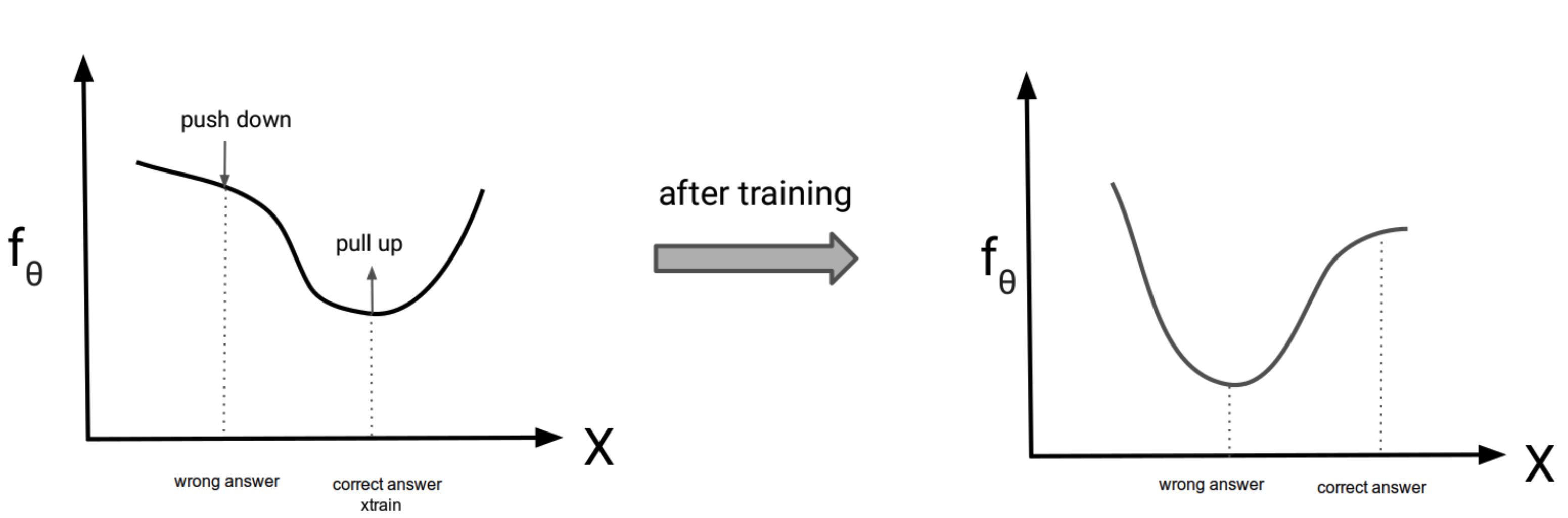
引用: https://deepgenerativemodels.github.io/assets/slides/cs236_lecture11.pdf

• VAEとの違い
  • VAEは確率分布を直接最適化しているわけではなく, ELBOを最適化している
    • イェンセンの不等式で出てくる例のアレ
    • cf. Prototypical Contrastive Learning of Unsupervised Representations
      • スライド