はじめに
先日, 研究室の勉強会で この本 のGibbs Samplingの章(9.3.4)を担当しました. 実際にpythonで実装してみたりしたので, せっかくですから備忘録程度にまとめてみました.
なお, 数弱によるガバガバ数学が展開されておりますのでご了承ください.
Markov連鎖 Monte Carlo法
ベクトル $\boldsymbol{x}$ が分布 $p(\boldsymbol{x})$ に従う際, 期待値を求めたいことが多々あります.
$$ \mathbb{E_{p(\boldsymbol{x})}}[f(\boldsymbol{x})] = \int f(\boldsymbol{x})p(\boldsymbol{x}) d\boldsymbol{x} $$
しかし, 右辺の積分計算が解析的に求まらない or 求めるのが難しいような場合, データ点 $\boldsymbol{x}$ をサンプリングしてくる必要が出てきます.
ここで, サンプル点をどのように生成するかが問題となってきます. まず素直な方法として, 一様に乱数を生成させ領域外のものだけを棄却する, もしくはそうしたサンプルに何らかの重み付けをするといった手があります. しかしそのような手法の場合, サンプルの次元が高くなると $p(\boldsymbol{x}) \gt 0$ の領域の外皮の部分からばかりサンプリングされてしまい(次元の呪い), 高次元の期待値計算には役に立ちません. したがって, 高次元空間におけるサンプリングでは $p(\boldsymbol{x}) \gt 0$ の領域からなるだけ均等にサンプルが生成されるという性質が要請されることになります.
そこで, 現在のサンプル点から次のサンプル点を連鎖的に生成するという手法が考えられます. そうした手法のうち, サンプル点の生成がMarkov過程であるような手法のことを特にMarkov連鎖 Monte Carlo法, 略してMCMCと呼びます.
Gibbs Sampling
Gibbs Samplingは, 簡単かつ強力にサンプリングが行えるMCMC法の一つです. Gibbs Samplingでは, 生成されたサンプル $\boldsymbol{z}^{(t)} = [z_1^{(t)}, … , z_K^{(t)}]^\top$ を各次元ごとに更新していき, 次のサンプル $\boldsymbol{z}^{(t+1)}$ を生成します.
具体的にアルゴリズムを以下に示します.
Algorithm
-
step0.
- $ t = 0 $ として $\boldsymbol{z}^{(0)} = [z_1^{(0)}, … , z_K^{(0)}]^\top$ を $p(\boldsymbol{x}) \gt 0$ の領域内から決める.
-
step1.
- for $ t $ in 1 … $ T $
- $ p(z_1 | z_2^{(t)}, … , z_K^{(t)})$ から新規サンプル $ z_1^{(t+1)} $ を生成
- $ p(z_2 | z_1^{(t+1)}, z_3^{(t)}, … , z_K^{(t)})$ から新規サンプル $ z_2^{(t+1)} $ を生成
- ….
- $ p(z_k | z_1^{(t+1)}, z_2^{(t+1)}, z_{k-1}^{(t+1)}, z_{k+1}^{(t)}, … , z_K^{(t)})$ から新規サンプル $ z_k^{(t+1)} $ を生成
- ….
- $ p(z_K | z_2^{(t+1)}, … , z_{K-1}^{(t+1)})$ から新規サンプル $ z_K^{(t+1)} $ を生成
- for $ t $ in 1 … $ T $
Metropolis-Hasting との比較
このように Gibbs Sampling では各次元ごとにサンプルを更新するので, サンプル点は以下のように隣接点と直交する形でジグザグに生成されていきます.
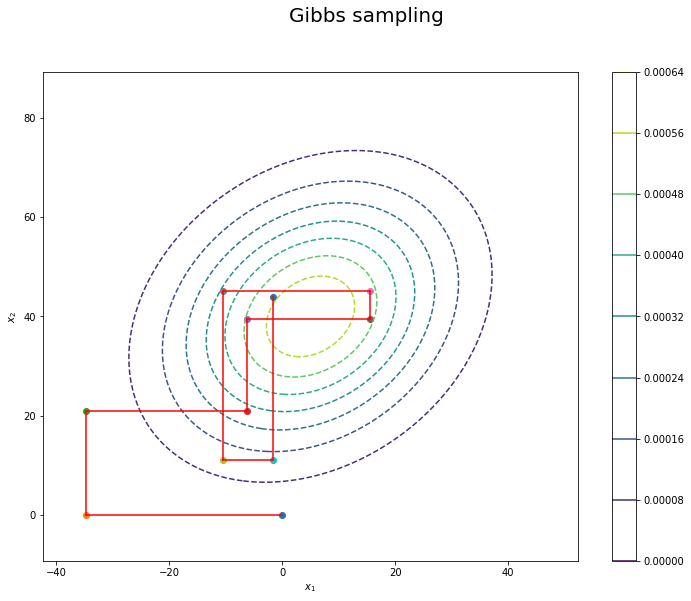
なお, Gibbs Sampling は Metropolis-Hasting から捉え直すことができます. すなわち, 同手法の判定関数を計算すれば, Gibbs Sampling は受容確率が $ 1 $ であるようなMetropolis-Hasting であると見做すことができ, Gibbs Sampling がより強力な手法である傍証が伺えます.
多次元正規分布におけるGibbs Sampling
では実際に, 多次元正規分布へGibbs Samplingを適応してみましょう. まずは上に示したアルゴリズムの通り, ある次元を更新対象とした際の条件付き確率 $ p(x|\boldsymbol{y}) $を計算していきます.
第一目標は, この条件付き正規分布のパラメタ $\sigma_{x|\boldsymbol{y}}^2 , \mu_{x|\boldsymbol{y}} $ を導出することです.
条件付き確率の導出
多次元正規分布は以下の式で記述されます.
$$ p(\boldsymbol{z}|\boldsymbol{\mu}, \Sigma) =\frac{1}{{(2\pi)}^{k/2}|\Sigma|^{1/2}}\exp\biggl[-\frac{(\boldsymbol{z}-\boldsymbol{\mu})^{\top}\Sigma^{-1}(\boldsymbol{z}-\boldsymbol{\mu})}{2}\biggr] $$
計算の都合上, 共分散行列 $ \Sigma $ を精度行列 $ \Lambda $ と置き換えておきます.
$$ p(\boldsymbol{z}|\boldsymbol{\mu}, \Lambda) =\frac{|\Lambda|^{1/2}}{{(2\pi)}^{k/2}}\exp\biggl[-\frac{(\boldsymbol{z}-\boldsymbol{\mu})^{\top}\Lambda(\boldsymbol{z}-\boldsymbol{\mu})}{2}\biggr] $$
ここで, $ \boldsymbol{z} $ を更新対象となる第一番目の変数 $ x $ と 第二番目以降の変数が格納される $ \boldsymbol{y} $ に分割し, 以下のようなブロック行列の形で記述します.
$$ \boldsymbol{z} = \begin{pmatrix} x \\ \boldsymbol{y} \end{pmatrix}, \boldsymbol{\mu} = \begin{pmatrix} \mu_x \\ \boldsymbol{\mu_y} \end{pmatrix} $$
$$ \Sigma = \begin{pmatrix} \sigma_x^2 & \Sigma_{x\boldsymbol{y}} \\ \Sigma_{\boldsymbol{y}x} & \Sigma_{\boldsymbol{y}\boldsymbol{y}} \end{pmatrix} $$
$$ \Lambda = \begin{pmatrix} \lambda_x^2 & \Lambda_{x\boldsymbol{y}} \\ \Lambda_{\boldsymbol{y}x} & \Lambda_{\boldsymbol{y}\boldsymbol{y}} \end{pmatrix} $$
このとき,
$$ p(x|\boldsymbol{y}) = \frac{p(x,\boldsymbol{y})}{p(\boldsymbol{y})} = \frac{p(\boldsymbol{z}|\boldsymbol{\mu},\Sigma)}{p(\boldsymbol{y})} \propto exp\left( - \frac{(x-\mu_{x|\boldsymbol{y}})^2}{2\sigma^{2}_{x|\boldsymbol{y}}} \right) $$
より, $ p(\boldsymbol{z}|\boldsymbol{\mu},\Sigma) $ から $ x $ についての二次の項, 及び一次の項の係数さえ取り出せれば良いことがわかります.
計算過程は省略しますが, 実際に計算すると
$$ \begin{cases} \sigma_{x|\boldsymbol{y}}^2 = \lambda_{xx}^{-1} \\ \mu_{x|\boldsymbol{y}} = \mu_x - \lambda_{xx}^{-1}\Lambda_{x\boldsymbol{y}}(\boldsymbol{y}-\boldsymbol{\mu_y}) \end{cases} $$
となることがわかります.
ここで, 上で導出した各パラメタが, 精度行列の小行列によって構成されていることに留意する必要があります. すなわち, この式を平均と共分散行列だけで記述するために, 精度行列を共分散行列によって書き下す必要が出てきます.
そこで, ブロック行列の逆行列を計算すると(補足参考),
$$ \begin{cases} \sigma_{x|\boldsymbol{y}}^2 = \mu_{x} + \Sigma_{x\boldsymbol{y}}\Sigma_{\boldsymbol{y}\boldsymbol{y}}^{-1}(\boldsymbol{y}-\boldsymbol{\mu_y}) \\ \mu_{x|\boldsymbol{y}} = \sigma_x^2 - \Sigma_{x\boldsymbol{y}}\Sigma_{\boldsymbol{y}\boldsymbol{y}}^{-1}\Sigma_{\boldsymbol{y}x} \end{cases} $$
となり, 無事に条件付き正規分布の各パラメタが導かれました.
というわけで, これらの結果から多次元正規分布におけるGibbs Sampling のアルゴリズムは以下のようになることがわかります.
Algorithm
-
step0.
- $ t = 0 $ として $\boldsymbol{z}^{(0)} = [z_1^{(0)}, … , z_K^{(0)}]^\top$ を決める.
-
step1.
- for $ t $ in 1 … $ T $
- for $ k $ in 1 … $ K $
- $ x $ を $ k $ 番目の次元と, $ y $ を $ k $ 番目以外の次元と対応させ, $ \sigma_{x|\boldsymbol{y}}^2 , \mu_{x|\boldsymbol{y}} $ を計算.
- $ p(z_k | z_1^{(t+1)}, z_2^{(t+1)}, z_{k-1}^{(t+1)}, z_{k+1}^{(t)}, … , z_K^{(t)})$ を パラメタ $ \sigma_{x|\boldsymbol{y}}^2 , \mu_{x|\boldsymbol{y}} $ を持つ一次元の正規分布とする.
- 上記の分布から新規サンプル $ z_k^{(t+1)} $ を生成
- for $ k $ in 1 … $ K $
- for $ t $ in 1 … $ T $
補足 : ブロック行列の逆行列
以下のようなブロック行列 $ P $ の逆行列を考えます.
$$ P = \begin{pmatrix} A & B \\ C & D \\ \end{pmatrix} $$
まず $ P $ をブロックLDU分解して,
$$ P = \begin{pmatrix} I & O \\ W & I \\ \end{pmatrix} \begin{pmatrix} X & O \\ O & Y \\ \end{pmatrix} \begin{pmatrix} I & Z \\ O & I \\ \end{pmatrix} = \begin{pmatrix} W & XZ \\ WX & WXZ+Y \\ \end{pmatrix} $$
$$ \begin{cases} W = CA^{-1} \\ X = A \\\ Y = D - CA^{-1}B\\\ Z = A^{-1}B \end{cases} $$
ブロック行列 L, D, U の逆行列を求めると,
$$ L^{-1} = \begin{pmatrix} I & O \\ W & I \\ \end{pmatrix}^{-1} = \begin{pmatrix} I & O \\ -W & I \\ \end{pmatrix} $$
$$ D^{-1} = \begin{pmatrix} X & O \\ O & Y \\ \end{pmatrix}^{-1} = \begin{pmatrix} X^{-1} & O \\ O & Y^{-1} \\ \end{pmatrix} $$
$$ U^{-1} = \begin{pmatrix} I & Z \\ O & I \\ \end{pmatrix}^{-1} = \begin{pmatrix} I & -Z \\ O & I \\ \end{pmatrix} $$
したがって, ブロック行列 $ P $ の逆行列は,
$$ P^{-1} = \begin{pmatrix} A & B \\ C & D \\ \end{pmatrix}^{-1} = \begin{pmatrix} I & O \\ W & I \\ \end{pmatrix}^{-1} \begin{pmatrix} X & O \\ O & Y \\ \end{pmatrix}^{-1} \begin{pmatrix} I & Z \\ O & I \\ \end{pmatrix}^{-1} $$
$$ = \left( \begin{array}{cc} (A - BD^{-1}C)^{-1} & -(A - BD^{-1}C)^{-1}BD^{-1} \\ -D^{-1}C(A - BD^{-1}C)^{-1} & D^{-1}+D^{-1}C(A - BD^{-1}C)^{-1}BD^{-1} \end{array} \right)$$
と書け, Woodburyの公式より,
$$ P^{-1} = \left( \begin{array}{cc} (A - BD^{-1}C)^{-1} & -(A - BD^{-1}C)^{-1}BD^{-1} \\ -D^{-1}C(A - BD^{-1}C)^{-1} & D^{-1}+D^{-1}C(A - BD^{-1}C)^{-1}BD^{-1} \end{array} \right) $$
$$ = \begin{pmatrix} T^{-1} & -T^{-1}BD^{-1} \\ -D^{-1}CT^{-1} & D^{-1}+D^{-1}CT^{-1}BD^{-1} \\ \end{pmatrix} $$
と書けます. (ただし $ T := A - BD^{-1}C $ )
以上より, 上式を共分散行列に適応して,
$$ \begin{cases} \lambda_{xx} = \sigma_x^2 - \Sigma_{x\boldsymbol{y}}\Sigma_{\boldsymbol{y}\boldsymbol{y}}^{-1}\Sigma_{\boldsymbol{y}x} \\ \Lambda_{x\boldsymbol{y}} = - (\sigma_x^2 - \Sigma_{x\boldsymbol{y}}\Sigma_{\boldsymbol{y}\boldsymbol{y}}^{-1}\Sigma_{\boldsymbol{y}x})^{-1} \Sigma_{x\boldsymbol{y}} \Sigma_{\boldsymbol{y}\boldsymbol{y}}^{-1} \end{cases} $$
実装
具体的なアルゴリズムが規定されたので, 実際に実装してみましょう.
まずは適当な分布を用意します.
|
|
描画してみると,
|
|
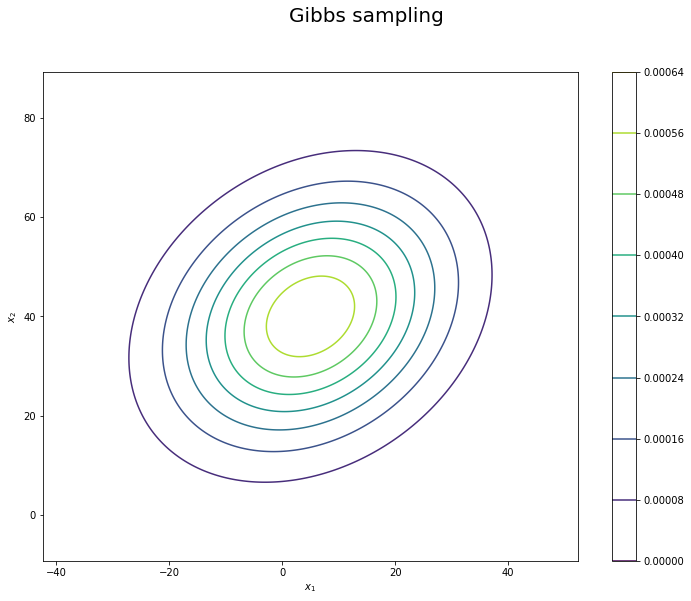
上で述べたように, Gibbs Sampling では更新対象の次元を随時入れ替えながらサンプルを更新していきます.
そこで今回は, 対象の次元を除くようなmask (idxs)を作って更新対象を計算することにしましょう.
|
|
$ N = 500 $ 回サンプリングを行った結果がこちらです.
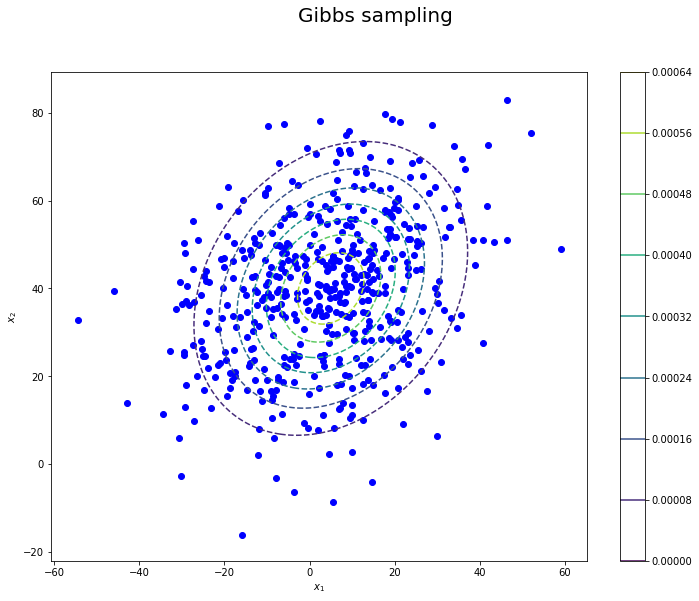
いい感じにサンプリングできています … !
更新過程の可視化
最後に, どのようにサンプルが更新されているのかを可視化してみましょう.
|
|
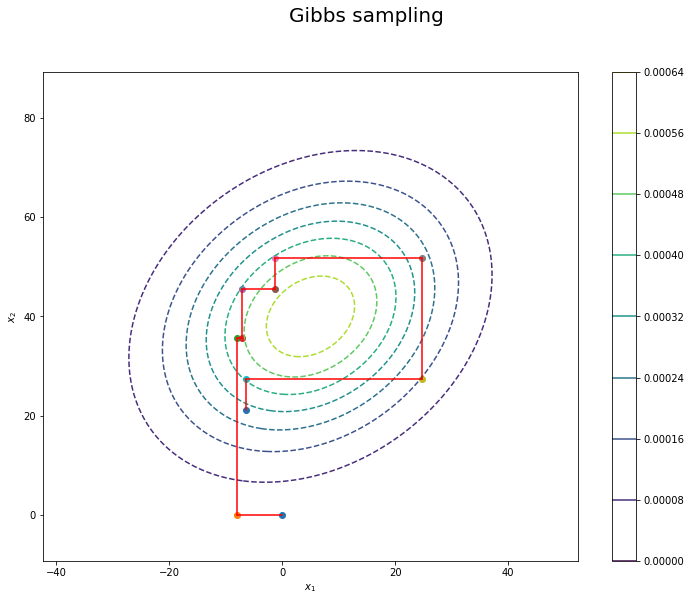
確かに, 分布に沿う形で各次元ごとにサンプルが更新されている様子を確認することができます.
おわりに
スライドのコメント部分に元のTex表記を貼っておいたので, 割りかし簡単に記事にできてよかった ✌
スライド ↓