【論文メモ】Graphormer: Do Transformers Really Perform Bad for Graph Representation? – 行李の底に収めたり[YuWd]

【論文メモ】Graphormer: Do Transformers Really Perform Bad for Graph Representation?

📅 2022/8/16 · ☕ 3 min read

はじめに

Transformerをベースとしたグラフ学習手法 (NeurIPS 2021)
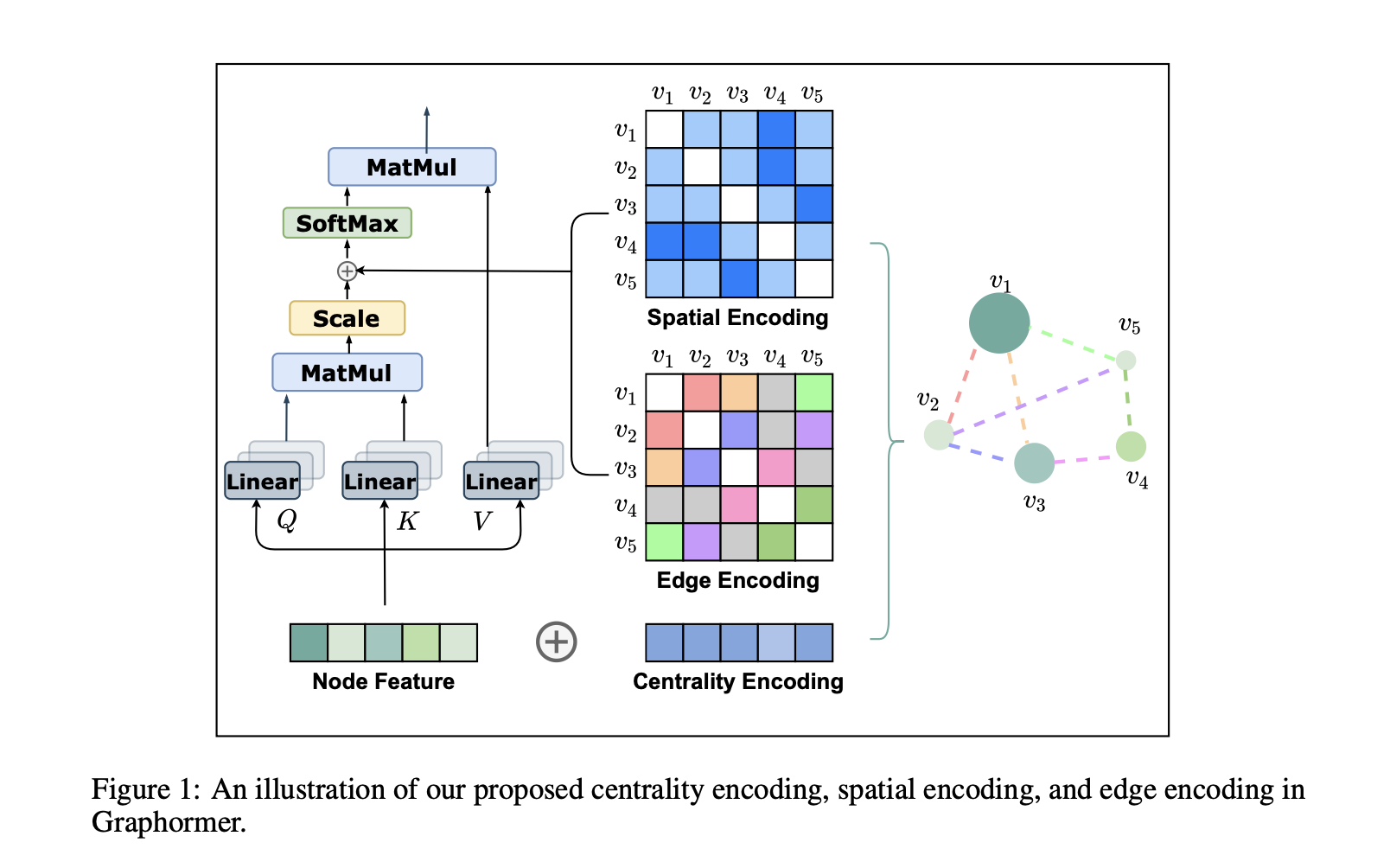
構成要素は三つ
- Centrality Encoding
- Spatial Encoding
- Edge Encoding (in the Attention)
特筆すべき点として, この手法はGINやGCN, それからGraphSAGEといったGNN手法を一般化したものとなっているらしい

Do Transformers Really Perform Bad for Graph Representation?

論文メモ

構成要素1. Centrality Encoding
- モチベーション
  - Node Centrality, つまりノードがどれほど別のノードとつながっているかはノードが如何に重要かを示しており, とても有益となり得るので, Encodeしたい
  - 例えばTwitterにおいて, 有名人はフォローが少なくてフォロワーが多い→ノードの次数は直感的にも重要
- どうするの？
  - ノードの埋め込み表現 $h_{i}^{(0)}$ について
    $h_{i}^{(0)} = x_{i} + z_{d e g_{(v_{i})}^{-}}^{-} + z_{d e g_{(v_{i})}^{+}}^{+}$
  - ただし, 入次数と出次数をそれぞれ, $d e g^{-}, d e g^{+}$ とする
  - 最初だけ( $h_{i}^{(0)}$ )なので計算コストもそれほどかからない
  - $z^{-}, z^{+} \in R^{d}$ は学習可能パラメタとなっていて, Centralityの埋め込みを行う
  - ただし無向グラフなら, $d e g^{-}, d e g^{+}$ を一つのパラメタ $d e g$ としても良い

構成要素2. Spatial Encoding
- モチベーション
  - Transformerの強さは受容野の広さだが, 一方でPositional Encodingが必要
  - どうにかGlobal-Attentionのまま位置情報を保存する形の写像がほしい
  - → GNNは隣接ノードしか見ない(AGGREGATE)なので, GNNよりも広い受容野を獲得できる
- どうするの？
  - ノード間の関係を $ϕ (v_{i}, v_{j})$ と記述し, QueryとKeyの内積=Attentionを以下のように変更
    $A_{i j} = \frac{(h_{i} W_{Q}) (h_{j} W_{K})^{⊤}}{\sqrt{d}} + b_{ϕ} (v_{i}, v_{j})$
  - Attention自体を修正している点に注意
  - 本論文では $ϕ (v_{i}, v_{j})$ を最短経路距離(SPD)とする
  - $b_{ϕ} (v_{i}, v_{j})$ は学習可能パラメタ (スカラ)
  - これにより, Attentionを $ϕ (\cdot)$ で調整できる
  - 例えば $ϕ (\cdot)$ に対して $b_{ϕ}$ が単調減少ならば, より周囲にAttentionを掛ける=隣接周囲を注視するようになる

構成要素3. Edge Encoding
- モチベーション
  - エッジの情報はもちろん重要. たとえば分子の解析などではエッジに結合情報が存在する
  - なので, エッジ $e \in E$ の特徴量 $x_{e}$ も埋め込みたい
- どうするの？
  - 最短経路をエッジ情報として埋め込む
  - →最短経路パス $S P_{i, j} = (e_{1}, e_{2}, \dots, e_{n})$ について, Attentionに $c_{i j}$ を追加
    $A_{i j} = \frac{(h_{i} W_{Q}) (h_{j} W_{K})^{⊤}}{\sqrt{d}} + b_{ϕ} (v_{i}, v_{j}) + c_{i j}$
  - ただし, $x_{e_{n}}$ を最短パス内のエッジ $e_{n}$ における特徴量として
    $c_{i j} = \frac{1}{N} \sum_{n = 1}^{N} x_{e_{n}} (w_{n}^{E})^{⊤}$
その他
- CLSトークン的な感じでVNodeトークンを追加
  - こいつはノードでもあって, 全てのノードとつながっている超頂点を成す
- 1-WL testで識別できないグラフでも, SPDを使えば識別可

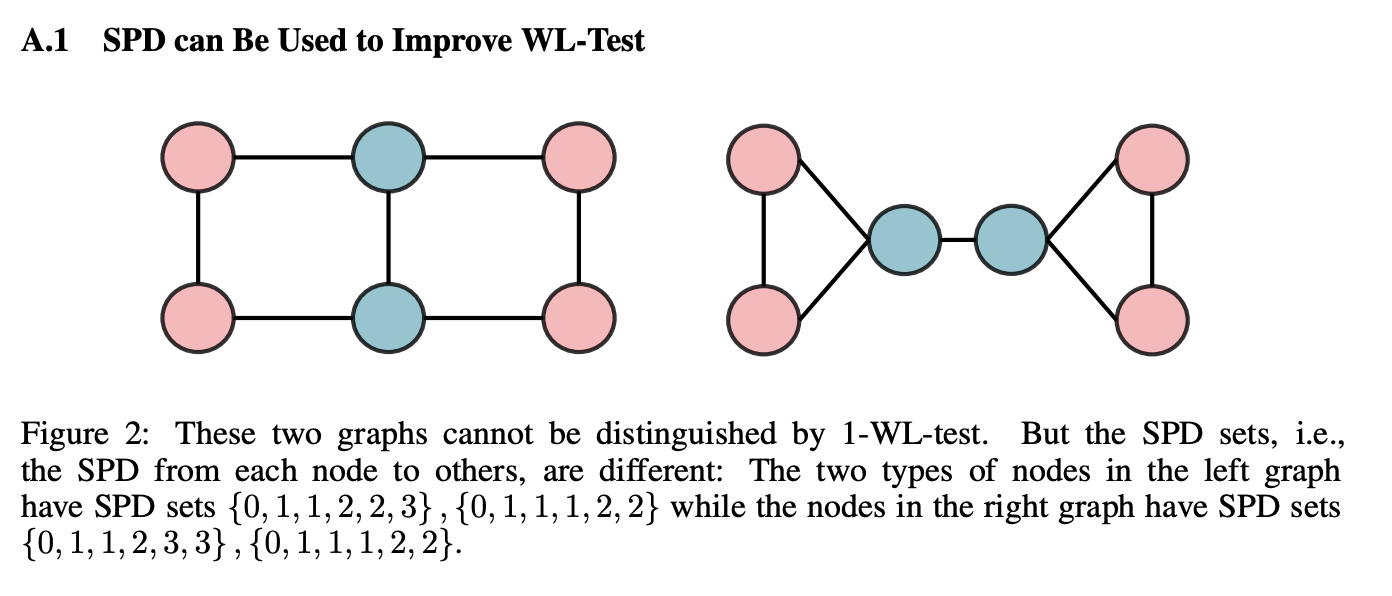
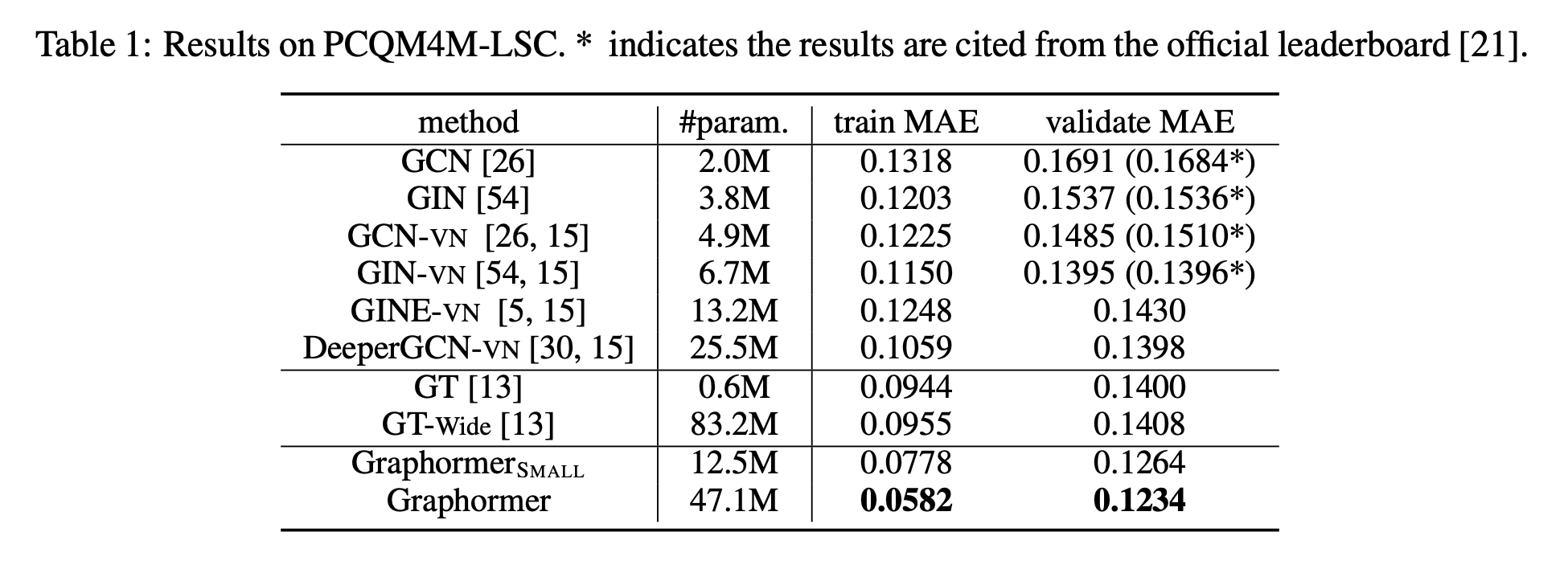
結果
- TokenGT (TokenGT: Pure Transformers are Powerful Graph Learners)と同じデータセットぽい？
- 確かに表現力は上がってそう
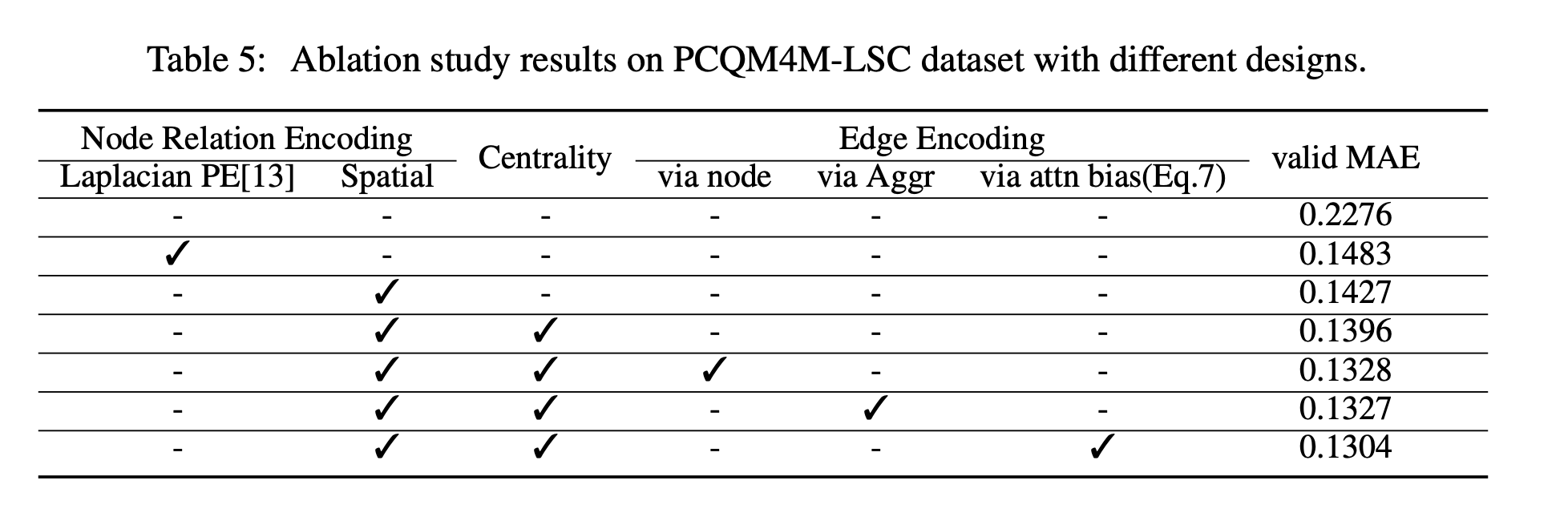
Ablation

Supplementary Material: https://openreview.net/attachment?id=OeWooOxFwDa&name=supplementary_material

共有

著者

YuWd (Yuiga Wada)

機械学習・競プロ・iOS・Web

関連記事