
-
モチベーション
- CLIPは単位行列を教師として学習する
- → バッチ内の負例同士にゆるい相関があった場合, 負例を全て0として学習するのは違うよね
- → 最適輸送問題を解いたものを教師として活用しよう
- OTTER (Optimal TransporT distillation for Efficient zero-shot Recognition) を提案
- Prototypical Contrastive Learning of Unsupervised Representationsと若干同じ感じ
-
loss
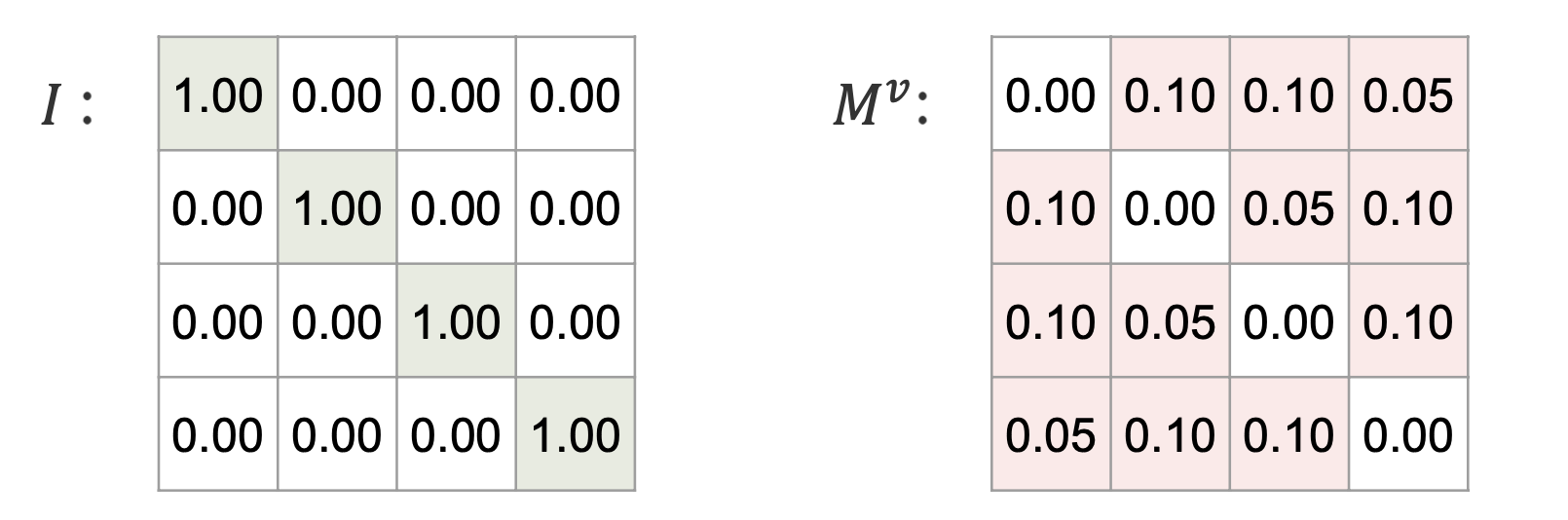
- 最適輸送問題
-
以下の式を解く (ただし最適輸送問題の双対問題となっている)
$$\mathbf{M}^{v*} = \argmax_{\mathbf{M}\in\mathcal{M}} \langle \mathbf{M}, \mathbf{S}^v\rangle_{F} + \lambda H(\mathbf{M}).$$ -
$\mathbf{S}^v$はテキストと画像の類似度
-
$\mathbf{S}^v = \gamma_{v} \mathbf{\tilde{Z}}^{v\top} \mathbf{\tilde{Z}}^v + \gamma_t \mathbf{\tilde{Z}}^{t\top} \mathbf{\tilde{Z}}^t + \mathbf{\tilde{Z}}^{v\top} \mathbf{\tilde{Z}}^t - \eta \mathbf{I}_N.$と定義する
-
画像の類似度 + テキストの類似度 + テキスト-画像間の類似度 - 単位行列
-
$\eta$は十分に大きい正の数で, この第四項により対角成分を0にできる
-
どうやって解くの?
- Sinkhorn-Knoppアルゴリズムを使えばOK
- 解は次のようになることが知られている
$$\mathbf{M}^{v*} = \text{Diag}(\mathbf{r})\exp(\mathbf{S}^v / \lambda) \text{Diag}(\mathbf{c})$$
-