
-
Optimizerの一つ
- ImageNetやCIFARを含む9つの画像分類データセットでSoTAを更新
-
SAMは損失が最小かつその周りも平坦となっているパラメータを探す
$$\min_{\mathbf{w}} L_\mathcal{S}^\text{SAM}(\mathbf{w})+\lambda|\mathbf{w}|_2^2$$ -
$L_\mathcal{S}^\text{SAM}(\mathbf{w})$ は以下のように定義. $L_\mathcal{S}$ は通常の損失関数. 何でもOK
$$L_\mathcal{S}^\text{SAM}(\mathbf{w}) \triangleq \max_{|\mathbf{\epsilon}|_p\leq\rho} L_\mathcal{S}(\mathbf{w}+\mathbf{\epsilon})$$ -
↑ 要はwの近傍まで考慮して最適化するので, 上図のように最小かつ周囲が平坦になる
- 最大化するεは一意に定まり, 解析的に求まるので, あとはその解に則ってアルゴリズムが定式化される
-
二回勾配を計算しないといけないので, 他の手法と比較する際はエポック数を2倍する必要があるので注意
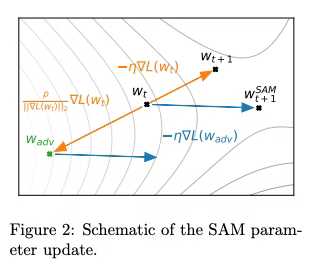
- 勾配を計算 (橙)
.2. 勾配のノルムを計算(全レイヤーまとめてスカラー値にする)- 勾配の逆方向に重みをずらす(ずらす量は2で計算したスカラー値に反比例させる) (橙)
- ずらした重みで勾配を再計算 (青)
- ずらした重みを元に戻す (青)
- 4で計算した勾配を使って、Optimizer(アルゴリズムはなんでもいい)を使って、重みを決定 (青)
引用: https://qiita.com/T-STAR/items/8c3afe3a116a8fc08429