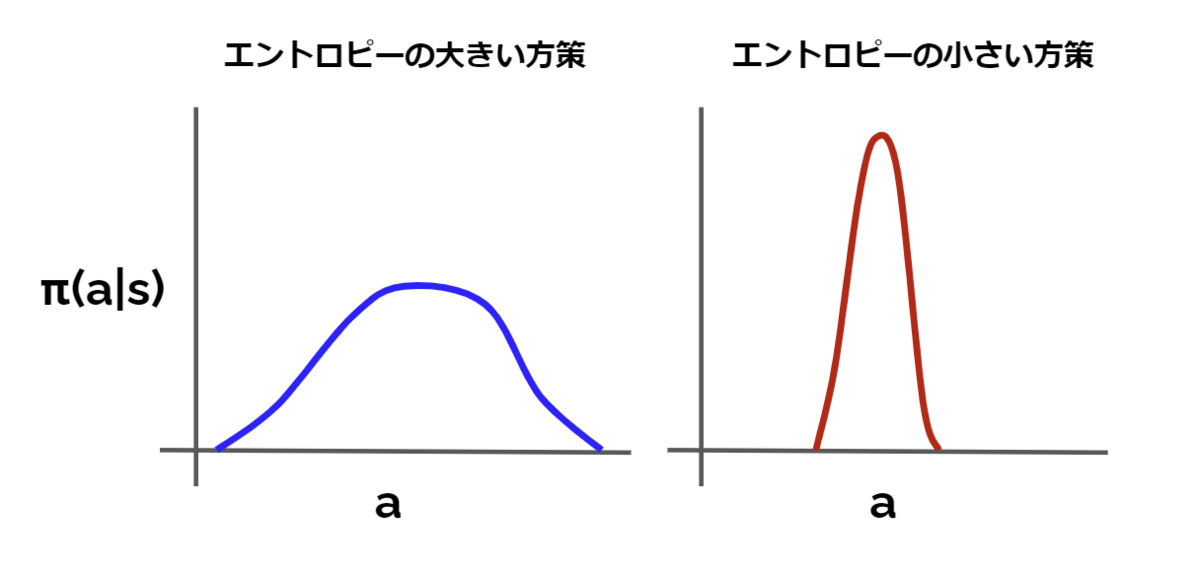
方策エントロピー
· ☕ 1 min read
探索空間において探索されたことで更新される情報量 情報エントロピー, もしくは方策の対数尤度の期待値と考えればOK $$\displaystyle{H(\pi( \cdot | s_t)) = \sum_{a} {-\pi(a | s)\log\pi(a | s)} = E_{a\sim\pi} \left[ {-\log\pi(a | s)} \right \rbrack}$$ 引用: https://horomary.hatenablog.com/entry/2020/12/20/115439 ...