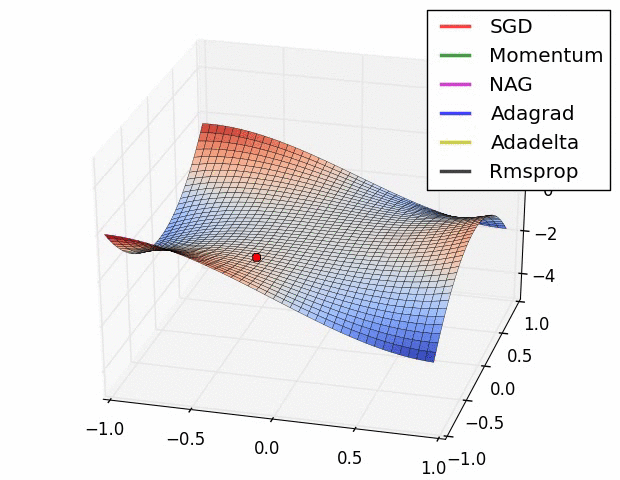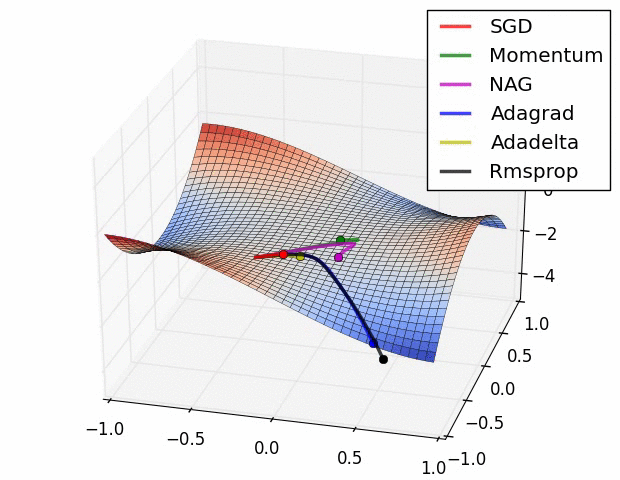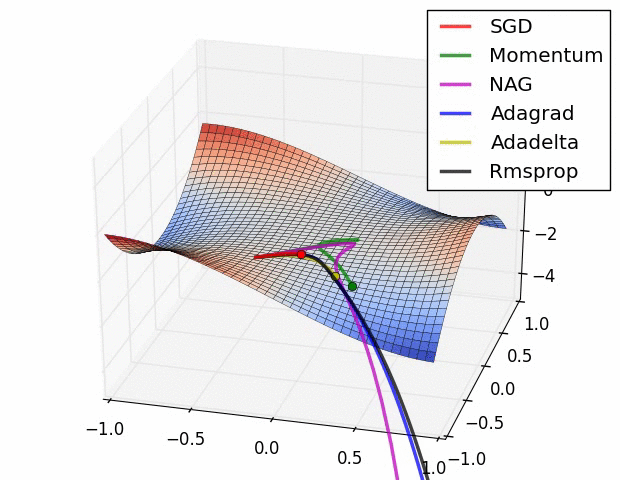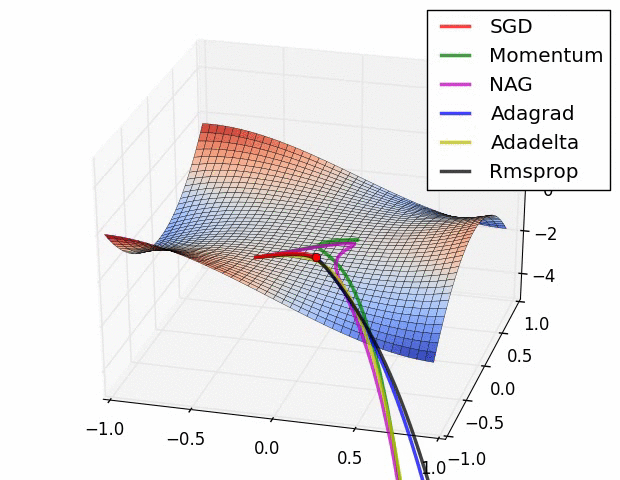
Distance CorrelationとPartial Distance Correlation について
· ☕ 4 min read
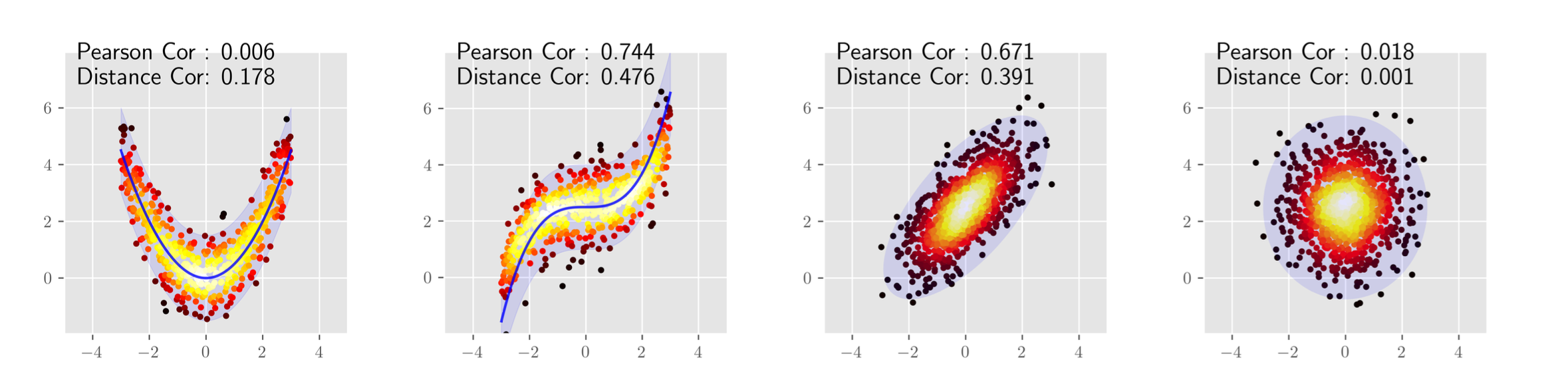
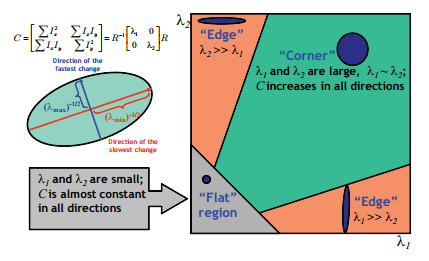
概要 pearsonの相関係数は線形な関係しか捉えることが出来ない. そこで, 点同士の距離を用いたDistance Correlationという相関係数が提案された. さらに, Distance Correlationを拡張し, 内積の期待値が共分散の二乗となるようなヒルベルト空間を定義したPartial Distance Correlationが提案されている. ...