はじめに
- ICLR22 [paper]
- 深層学習において, 残差接続は不可欠な存在となりつつある
- 残差接続により, より深い層数のNNを実現できるようになった
- 残差接続に対する解釈の矛盾
- 昨今の研究により残差接続は比較的浅い層をアンサンブルするような効果があるとの見方が強まっている
- しかし, 「深層」学習という名が体を表す通り, 一般には「層を増やす」ことがモデルの表現力を高めていると言われており, ここに残差接続に対する解釈の矛盾が存在する
- また残差接続は推論時においてメモリを圧迫しているとの見方も存在する
- 残差接続が結合されるまで, 入力を保持する必要があるため, 一つのスキップでメモリを倍使う (下図参照)
- 例えば, 残差接続はResNet-50における特徴量の40%もメモリを使用している
- 深層学習において, 残差接続は不可欠な存在となりつつある
- したがって, 残差接続の再考が必要であり, 残差接続を用いず層を増やす手法としてTATを提案
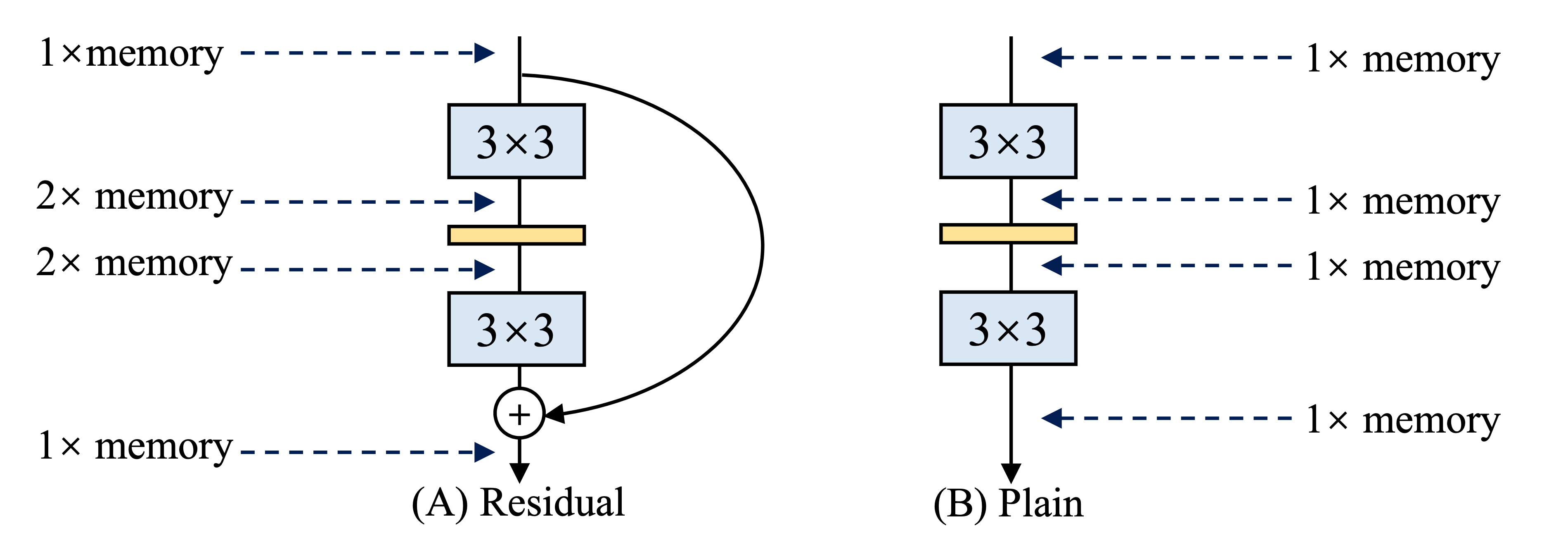
引用: RepVGG: Making VGG-style ConvNets Great Again
カーネルの近似
- 活性化関数を
- ただし, 重みは
- このとき,
- ネットワーク
- 各層ごとの
- (幅を無限大に飛ばす→NTKが想起されるが, NTKとは若干異なる)
Q/C maps
-
Q map
- ただし,
- このとき,
- また
- カーネル
-
C map
- 一方で
-
ただし,
-
非対角成分
- つまり, location-wiseな入力の類似度を計算することになる
-
こちらも同様,
- この関数は
- Cが線形であればあるほど活性化関数も線形に近づく (14.3)
- 線形だと, 類似度をそのまま出力してる = 線形
- 逆に
- 例えば ReLUを使った1層のネットワークの場合↓
- この関数は
- 一方で
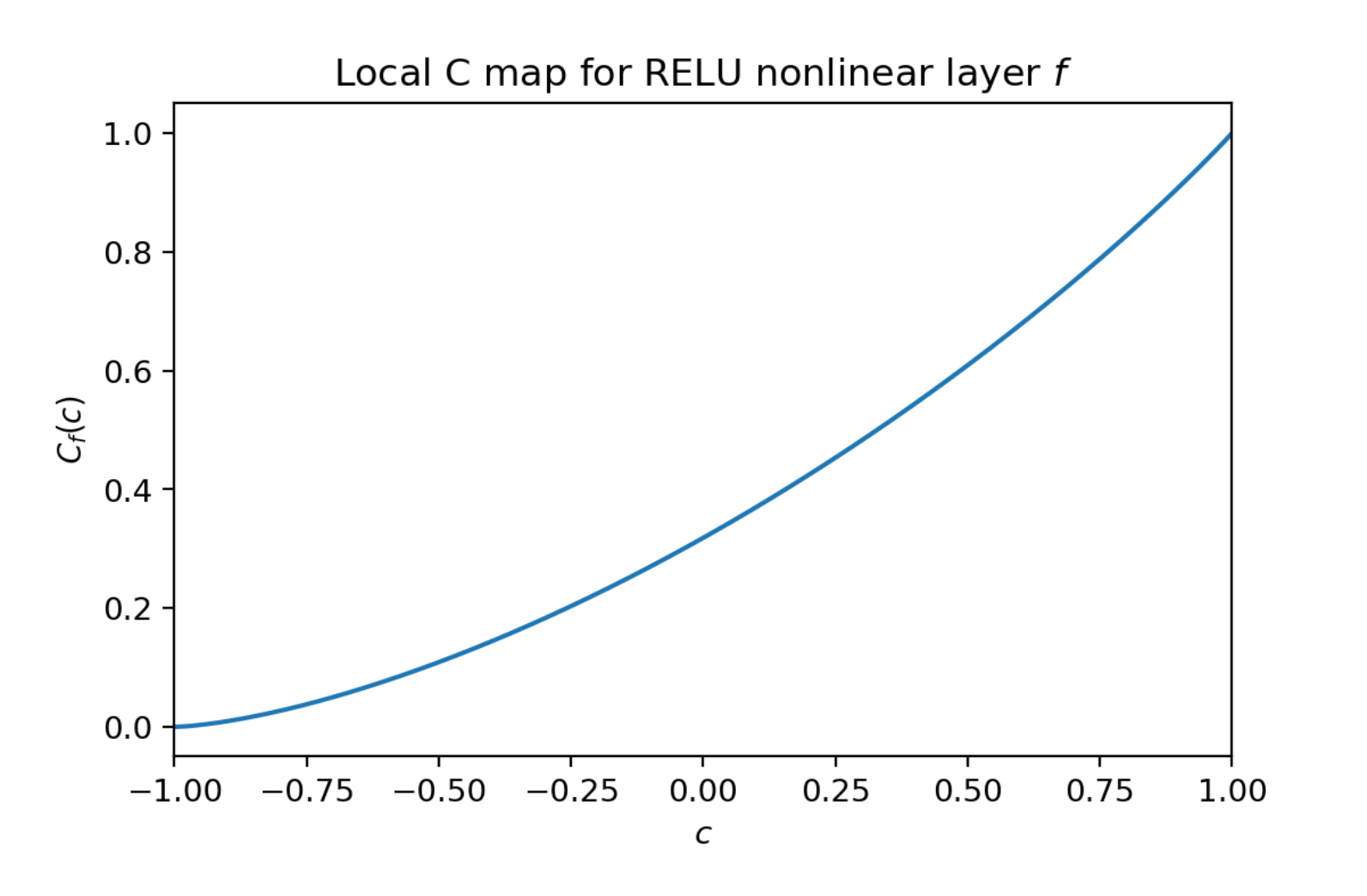
- これが何層にも連なると, C mapの値は1へと収束し, 単純に層を増やすだけでは学習が困難になる傍証が得られる↓
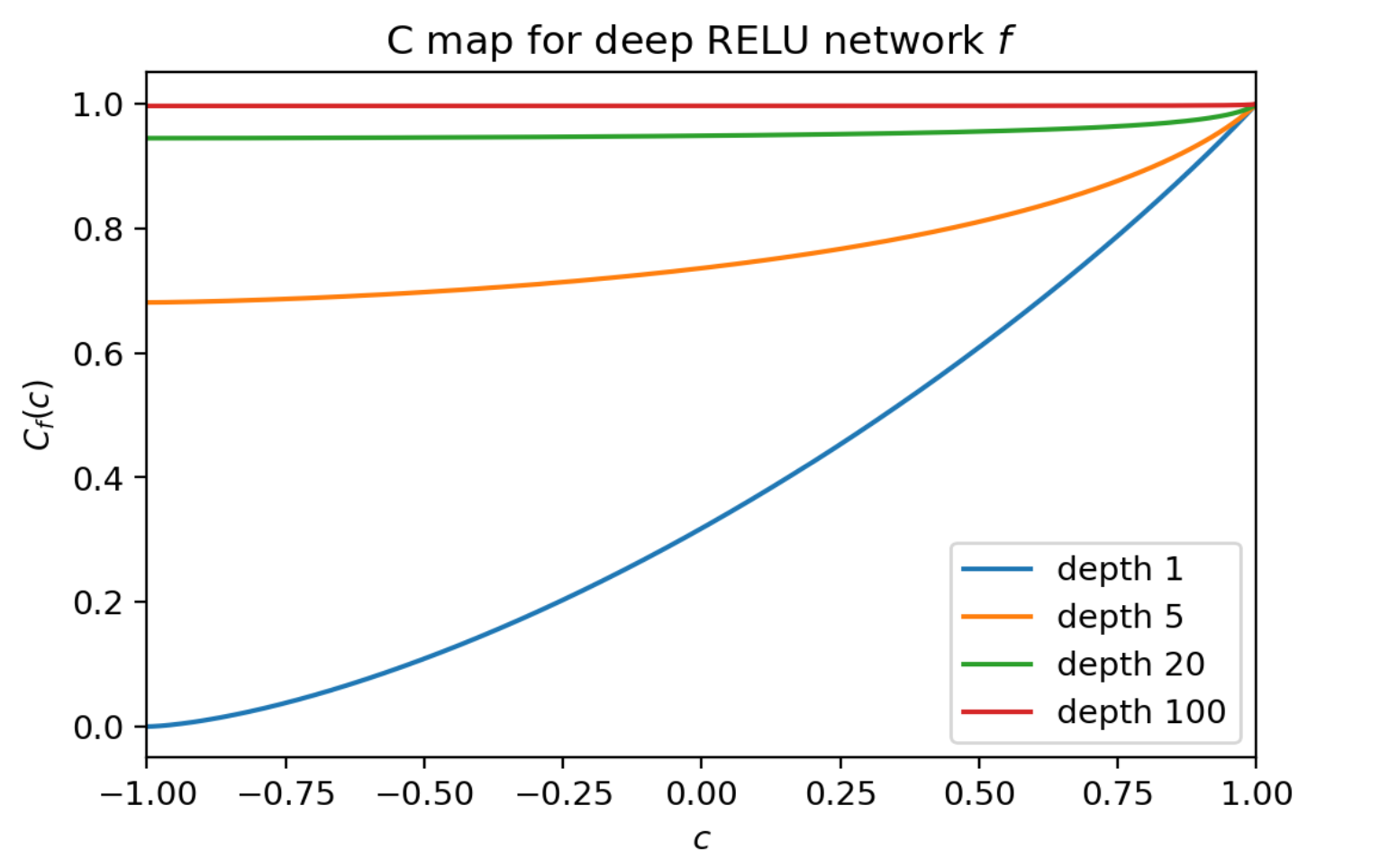
引用: Rapid training of deep neural networks without skip connections or normalization layers using Deep Kernel Shaping
Tailored Activation Transformation for Leakly ReLU
- Leakly ReLU (LReLu)
- という活性化関数を定義すると,
-
が成り立つ. (
-
- 各層の入力に対して, 摂動に強くなる方向へ制約がかかるため, カーネルの近似誤差が小さくなる
- ここについてはあまりよくわかっていない
-
- そこで,
- そこで,
-
以上より,
-
を満たすことができるように
-
そのようなLReLUのことをTReLUと呼び, 活性化関数をこのように変化させる手法としてTailored Activation Transformation(TAT)を提案
-
また, このような
-
TReLU計算アルゴリズム
-
目標:
-
このとき,
-
-
-
このとき,
-
より,
アルゴリズム
-
-
次に,
-

一般化アルゴリズム
- LReLUだけでなく, 一般に滑らかな活性化関数であれば同様の手法を用いることができる

評価
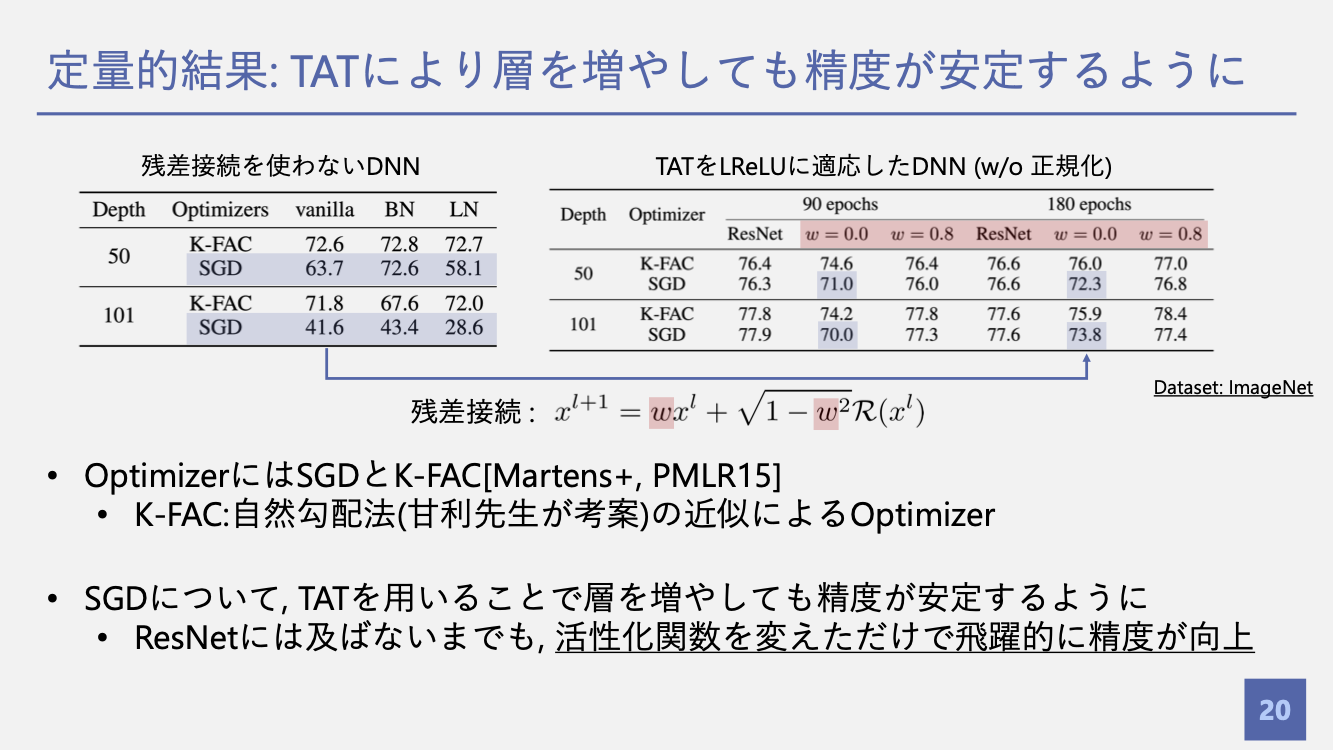
ロジックの整理 & misc
-
FFNにおけるカーネルを用意する→二次のGram行列の漸化式でカーネルの近似解が求まる→対角成分と非対角成分をそれぞれQ/C mapsと呼び, 入力の振幅と類似度を図る指標となる→ネットワーク全体における global Q/C mapsが理論解析のための道具となる
-
理想的なQ/C mapsの値が存在→maximal slope functionでサブネット全体を最適化
-
C mapを最大化するサブネットワークを探す
-
-
-
論文中に
|
|