本記事ではなく動画の視聴の方を推奨します.
概要
- ICLR23
- 状態空間モデル(state-space model; SSM)は様々なモダリティにおいて有用性が検証されてきたが,未だ言語系においては確認できていない.
- また,SSMは
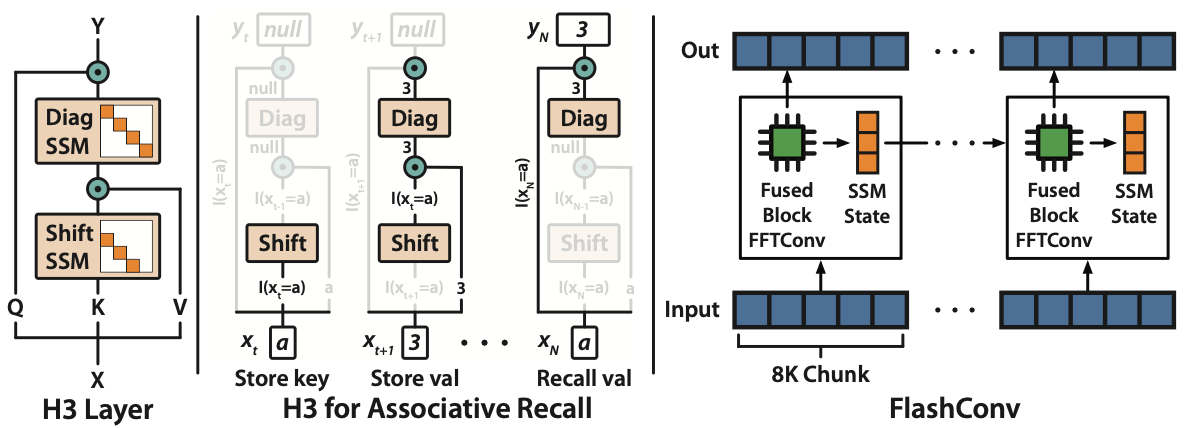
- 実験によって,SSMが①前方にあるトークンの記憶と②トークン間の比較が苦手なことを発見し,この二つの難点を乗り越える新たなSSMとしてH3 (Hungry Hungry Hippos)を提案する.
- Transformerに替わるモデルとも言われている(要出典)
SSMにおける二つの問題点
- 問題点①②を検証するために,二つのタスクInduction HeadとAssociative Recallを実施
- Induction Head : 特殊なトークン
|-で囲まれた部分文字列の先頭の文字を出力させるタスク- 前方のトークンを如何に覚えているかを測ることができる
- Associative Recall : key-valueでセットになってるアルファベットと数字の組に対して,与えられたkeyに対応するvalueを出力させるタスク
- この場合
a 2 c 4 b 3 d 1に対して入力がaなので2が答え (間違ってたら教えてくれ) - トークン間の関係を覚えているかどうかを測ることができる
- この場合
- Induction Head : 特殊なトークン

- 結果は以下の通り
- Attentionは100%成功しているが,従来手法はほとんどできていない
- 提案手法であるH3はほぼ100%成功
- Attentionは

先行研究について
- 具体的な手法に入る前にH3の系譜について述べる必要がある.
- H3は以下のような経緯で提案された
- HiPPO論文→LSSL→S4→H3
- 次章より,まずはHiPPOについて,それからLSSL / S4について軽く紹介する.
HiPPO (higher-order polynomial projection operators)
-
HiPPO: Recurrent Memory with Optimal Polynomial Projections (Gu+., NeurIPS20)
-
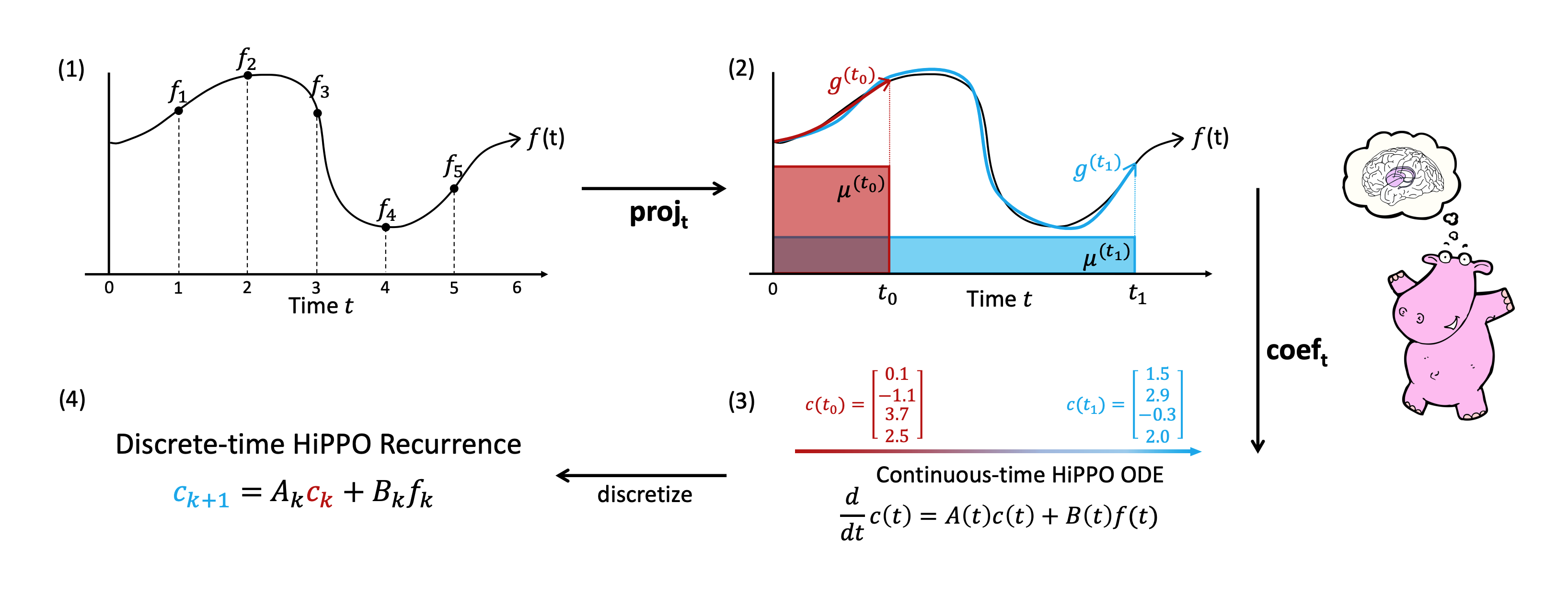
HiPPOは複数の直交多項式によって入力信号を近似する手法
-
(1)入力信号に対して,(2)で直交多項式(基底)
- この処理を
- 入力信号
- この処理を
-
(3)で,ある測度に対する基底
- この処理を
- この処理を
-
このとき,
- つまり,
- つまり,
-
この時,係数
-
ただし,
-
実験では,測度
-
このとき,連続空間では以下が成り立ち,
- 離散空間では以下が成り立つ.
- ただし,
- このとき,
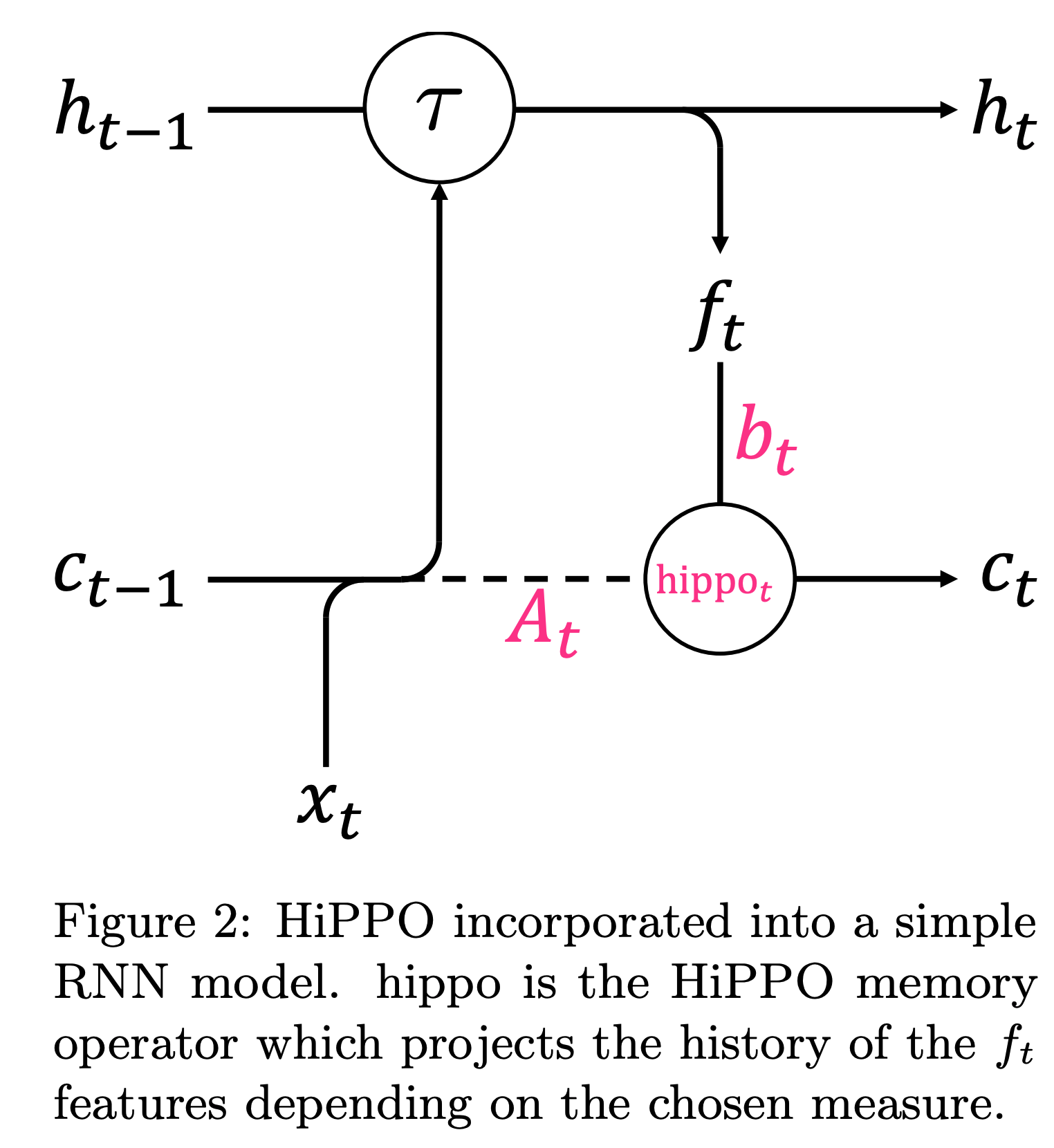
- hippoを組み込むだけで,劇的に精度が向上する
LSSL

-
Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (Gu+., NeurIPS21)
-
状態空間モデルにHiPPOを導入し,recurrent + conv. の両方で処理できる手法LSSLを提案
- RNNs: 系列データの学習に向いているが,勾配消失などの問題より長距離系列の学習に限界あり
- CNNs: 高速かつ並列可能だが,系列データの学習に向いていない
- NDEs: 連続時間かつ長距離依存を扱うことができるが,効率が悪い
-
これら3つのパラダイムを状態空間モデルによって統合的に扱うことを目標とする.
-
状態空間モデル
-
GBTにより離散化 (GBT; generalized bilinear transform)
-
-
-
以降,
-
また,LSSLは畳み込みで記述することもできる
- ここで,

S4

SSMの改善
-
SSM
-
①前方トークンの記憶
- shift演算(e.g.,
- 例えば,常に
- shift演算(e.g.,
-
②トークン間の比較
- Attentionと同様,
- 対角行列の初期化はこちらを参照.
- HiPPOについては以下を参照
- Attentionと同様,
-
最終的には以下のように設計
- 計算量の観点からEfficient Transformer系列に倣って,以下のように設計
- すなわち,
- 計算量の観点からEfficient Transformer系列に倣って,以下のように設計
The shift SSM can detect when a particular event occurs, and the diagonal SSM can remember a token afterwards for the rest of the sequence

- H3の流れ
- 入力
- 各headごとに
- headをconcatして最終的な値を得る.
- 入力
