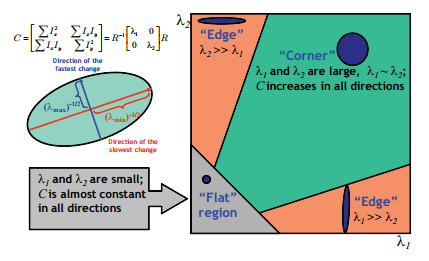
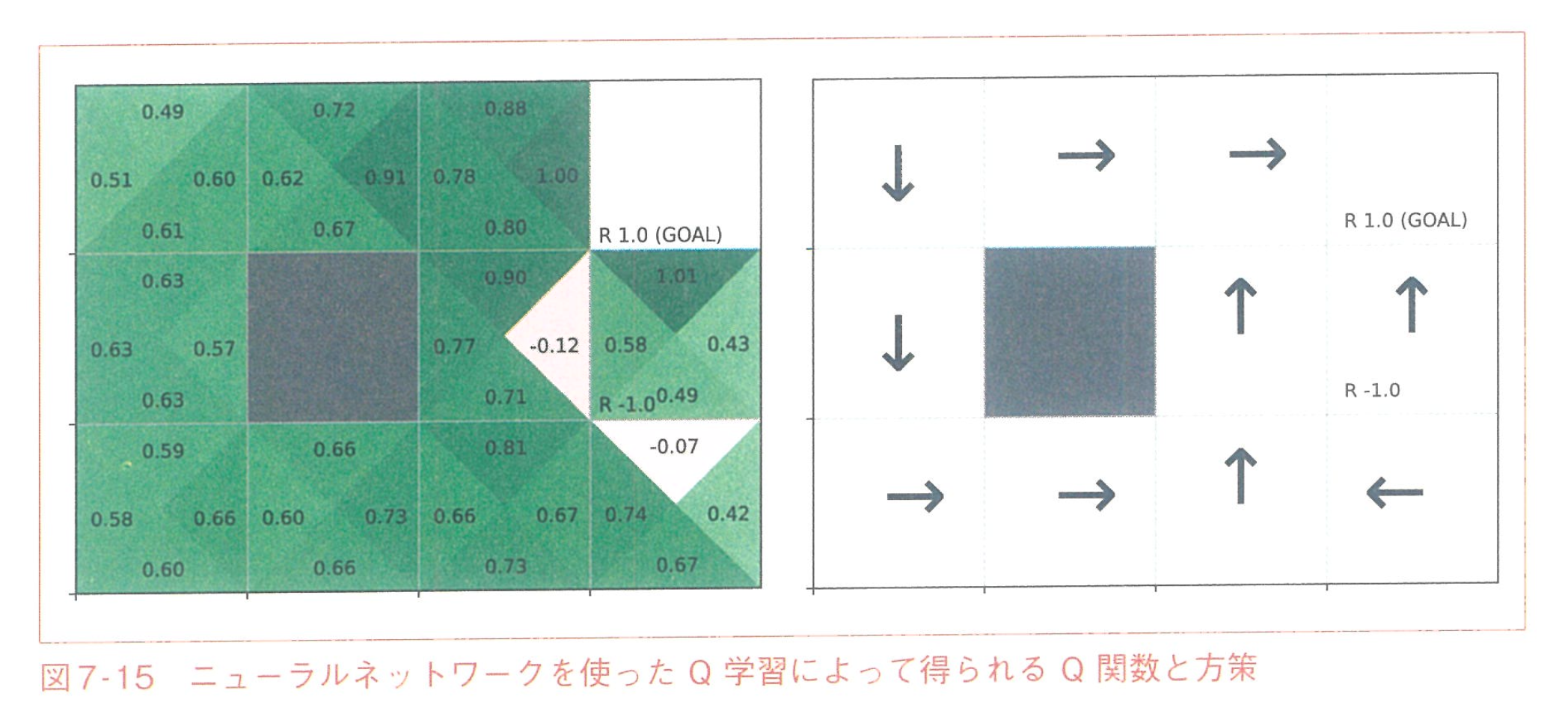
WikipediaのTexをコピペする
· ☕ 1 min read
WikipediaはMathJaxを使っているので(ホントか?), 画像を新規タブで開けばタイトルにtex表記が記述されている なので, 画像を新規タブで開く→ソースコードを表示→titleタグの部分をコピペすればOK 例 $${\displaystyle \langle S\rangle ={s_{k_{1}}^{e_{k_{1}}}s_{k_{2}}^{e_{k_{2}}}\cdots s_{k_{m}}^{e_{k_{m}}}\mid \exists m\in \mathbb {N} ,(k_{1},\ldots ,k_{m})\in \mathbb {N} ^{m},e_{k_{j}}\in \mathbb {N} ,s_{k_{j}}\in S}.}$$ ...