- 貪欲
- deque
- スタック
- キュー
- グラフ化 (Graph)
- BFS
- DFS
- Bit全探索
- DP
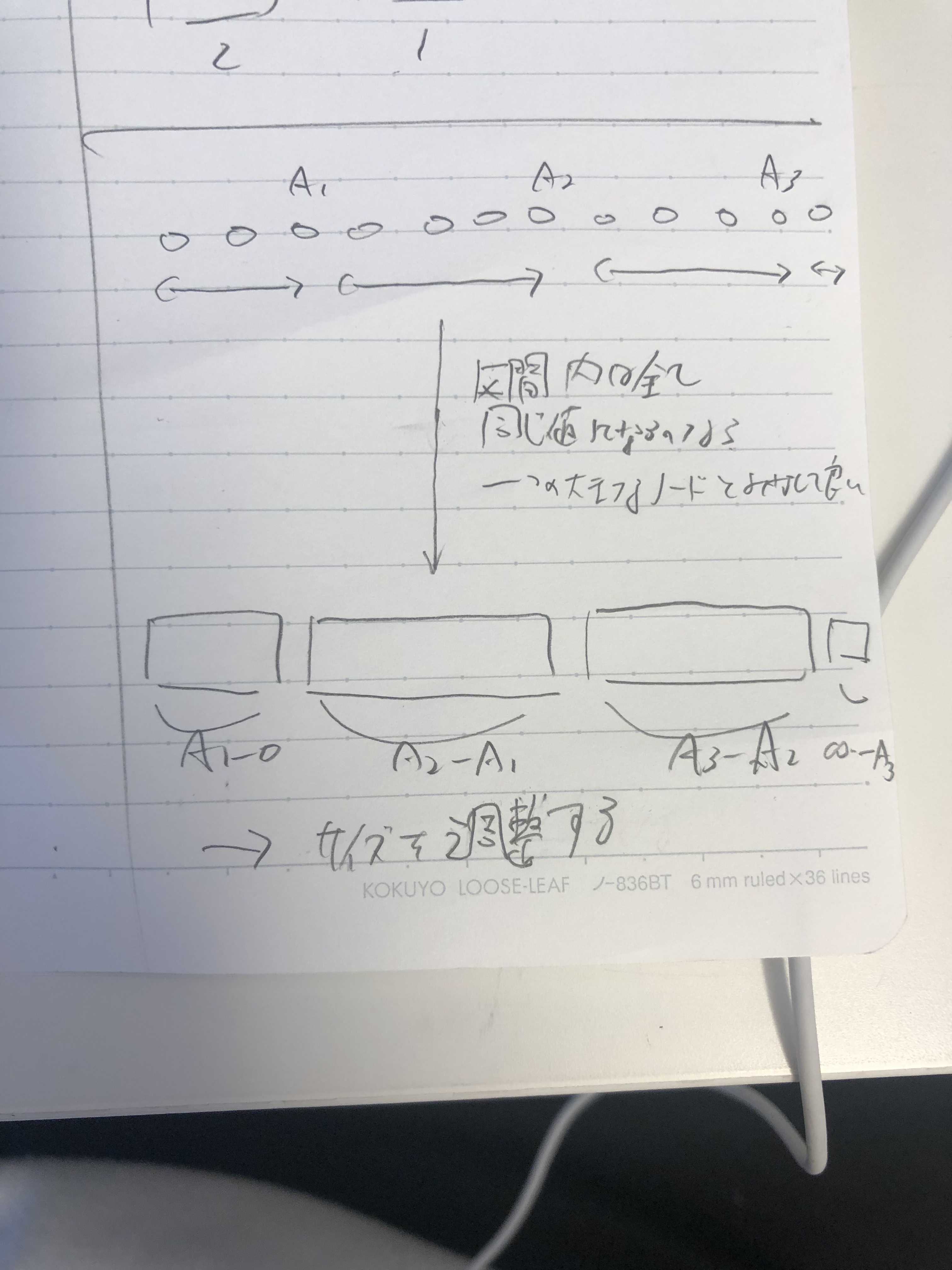
- 累積和
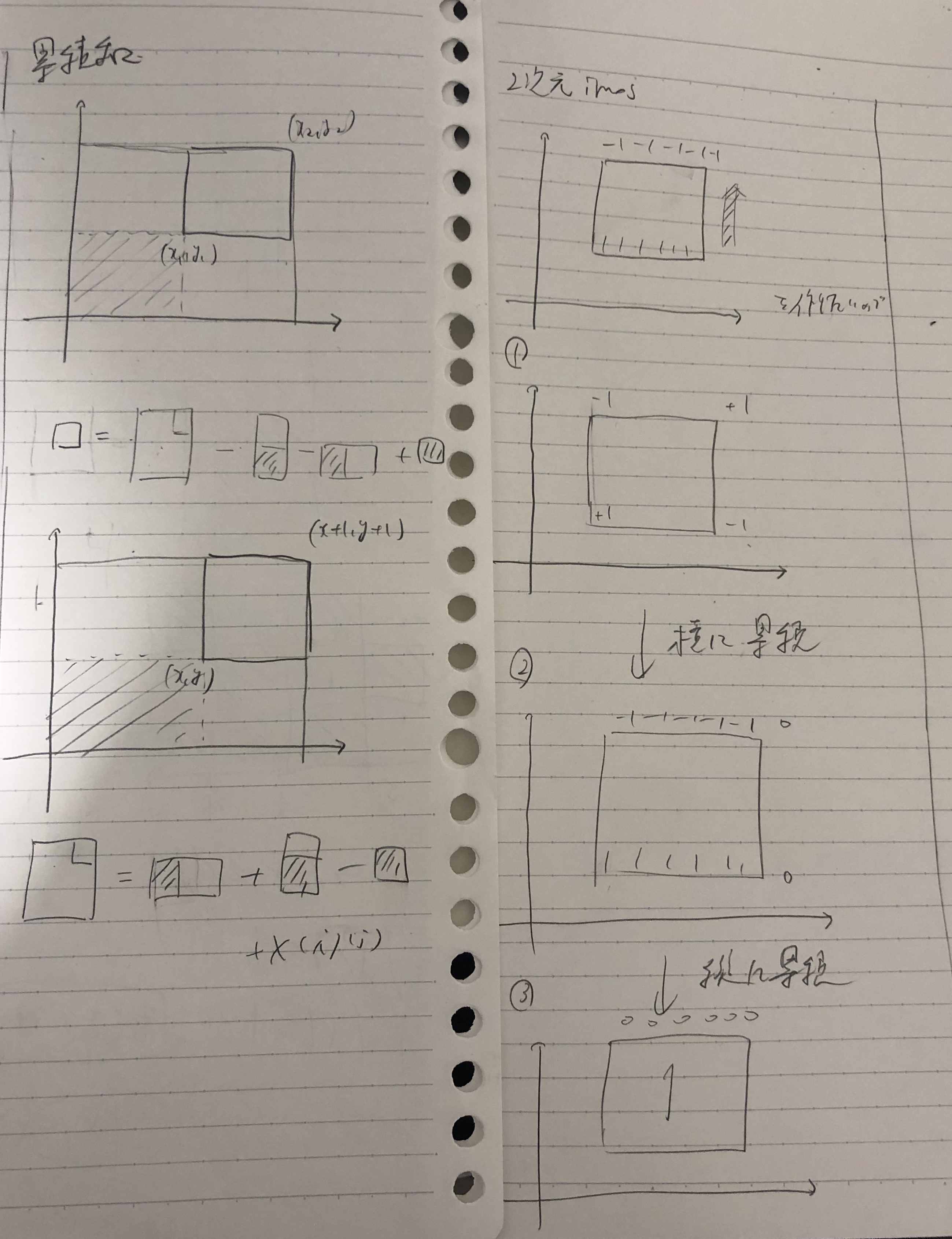
- 二次元累積和
- 尺取法
- 二分探索
- Union-Find
- ソート
- ダイクストラ
- ベルマンフォード
- ワーシャルフロイド
- 最小全域木
- PQ
- セグ木
- 最大流
- スター型グラフ
- 二次元座標を二部グラフにする(ABC 131 F)
- dpはとりあえず立式したほうがいい
- Dpは解けなそうで何でも解けるので、亜種dpを徹底的に試すと良い
- ダブリング
- 行列累乗
- 形式的べき級数 (FPS)
- 45℃回転
- imos法
- 調和級数で計算量落ちないか
- 番兵
- BIT
- bitset
- 平面走査 = x軸(もしくはy軸)でソートして小さい順に見ていくヤツ
- 偏角ソート → atanの扱い方に注意
- 複素数平面(ABC197D) → とにかく回転に強いので, 回転なら複素数
- 座標平面を回転させる (ABC139 F)
- マージテク
- 再帰
- 二分探索 → 「k番目の数」や「〜がk個」みたいな問題で使える (ABC 143)
- 拡張ダイクストラ, 超頂点
- 判定問題は論理式に直すといい → ∀ 等
- 牛ゲー → 不等式の制約がいっぱいある時に使える
- 場合分け (ARC 107 D)
- 計算量を√Nに落とす (ARC 60 D)
- 文字列群を連結して辞書順最小にする → 「x < y ⇔ x + y < y + x」
- ロリハ → 任意の区間のハッシュをO(1)で取得可能
- 二部マッチング (maxflow)
- 割ったり余りを計算したりするなら M進数
- HL分解 → 根方向に戻る時に逆元がないなら、オイラーツアーじゃなくてHL分解
- オイラーツアー → 辺verの場合は辺パス / 頂点verの場合は部分木系
- 行列 → アフィン変換風にダミーの次元を作ると、加算も表現できる(同次座標系)
- 行列累乗 = 遷移の係数がiに依存しないDPはコレ。 特に二項間の場合は、ダミー次元があると良い(ARC 20 C)
- 「連結成分の個数 = 頂点数 - 辺の数」(グラフが森ならば)
- A + B = (A xor B) + 2(A ∧ B)
- 操作をグラフに落とし込んでみる (JOI 2020/2021 第2問)
- クエリ平方分割 → ブロックの出入り / ブロック内の処理 を意識すると良い
- 巡回シフトは2周期分で考える (ABC 150 F / maspy解説)
- Kの倍数 -> mod Kのグラフで考える。(ARC 84 D)
- 全ての整数は1に対して + 1か x10 の操作を繰り返すことで作れる(ARC 84 D)
- マンハッタン距離が最小となる点は、例の中央値問題に帰着される
- 中国剰余定理 = CRT
- 自明なケースを除けば不等式が作れて有利に働くことがある (AGC 026 B)
- 区間がソート済みかどうかはO(1)で確認できる → AGC038 Bの自分のコード参照
- 区間問題 → 左端ソートするとうまくいくことがある
- 期待値の線形性
- 最長路問題 → DAGならトポロジカルソートすれば線形に解ける (D - Restore the Tree)
- トポロジカルソート (辺の見方: ソート済みの頂点集合を前から順に見ていけばg.get_edgesで辺取れる)
- 部分文字列問題は基本的にはO(N)で解けるみたい (けんちょん参照: next~ みたいなの使うやつ)
- 重複する要素のIndexをvector取るといいことが多い(pos みたいなやつ!)
- 接続行列(opt参照)に対してEに関する操作をすれば(=xをかける)、頂点に関する特徴ベクトルが取れる
- クソデカセグ木 → ノードのサイズを恣意的に取れば座圧で対応できる (ARC 115 E)
- セグ木でindexがほしい → セグ木に載せたデータとindexを紐付けたpairlを用意すれば良い(それか1e9*iを足しておいて, セグ木内処理のときに逐一1e9を消したり増やしたりするか)
- osak法 高速素因数分解
- マージテク(小→大 で O(log n))
- 木の直径
- MaxFlow
- MinCostFlow → 流量だけでなくコストを設定して、コストの最小値を計算できる
- 同じ遷移のdpは行列累乗
- スライド最小値
- OEISで検索!
- 01の場合、a xor b = a(1-b) + b(1-a)
- 超頂点
- Lucasの定理 → 素数modでcomb
- popcount
- 二部グラフ判定はUnionFind(noshi参照)か DFS(始点の色を決めてDFSすれば良い)
- パリティ(偶奇)を考える
- 最小値の最大化は二分探索 → 数直線・論理式に展開してみると意味がわかる.
- XORで任意の値が作れる → その集合を行列で表現した時, 行基本変形で単位行列的な感じになるか → 基底のサイズがnかどうか → XORの掃き出し法(noshi基底)
- 区間 → しゃくとり法
- 積の和 ΣΠ → FPS・約数
- 無理やり場合分け(桁DP・ARC)
- 木の最短パス → オイラーツアー
- 集合zに対しx⊆y⊆zな組(x,y)はちょうど3^z個( 4^zが3^zになるやつ)
- 連続する自然数の構築問題 → 2進数的にやる (+1 or x 2で全ての整数は表せる)
- Gcdのカウントは前から順にやれば良い
- 区間内の[x,y)を満たす値の出現数 ⇒ Wavelet Matrix (区間内xの出現数だけなら, 普通にposを持てばOK / ABC 202)
- 解を成長させる.(ルンルン数, AGC013B, ARC118)
- LISはin-placeに出来る
- SCCしたあと, 強連結成分自体を頂点としたグラフを作成する. (典型59)
- 平均値の最大化は二分探索
- 三分探索
- Nと互いな素な数の個数はオイラー関数 でO(√n))
- 約数系はゼータ変換・メビウス変換
- 約数の個数は少ない (1e9以下で最大1333個くらい)
- → 素因数の種類数はもっと少ない (1e5以下で高々6個 → bit全探索 + 包除原理があるある)
- 互いに素な組を探す → 素因数の組み合わせの積 mul に対して, mul, 2mul, 3mul, … という数列から, 包除原理を用いてgcd = 1(一つも素因数にかぶりが無い)であるものを出す
- Maspy式桁DP→ f = count{Xの集合} として, S(=Xの集合)からXの場合分けをすれば良い ABC208 E
- → 集合を場合分けして再帰にもちこむ
- 愚直に考える
- 桁DPは $dp[i\rbrack - S[i\rbrack$ で, i <-> i と対応付けた方がやりやすい?
- マッチング問題 → ホールの定理(結婚定理)
- 貪欲 → 損するかどうか
- Baby-step Giant-step → 離散対数問題: A^x ≡ B (mod M) を満たす最小のx
https://algo-logic.info/how-to-think-cp/#toc_id_17
memo
- ギリギリオーバーフローしそうになったら__int128 を使う
- OEISでエスパーするときは「第3項目あたりから5,6項を入れて検索する」と良い
期待値問題
-
- 後ろから前にいくにつれて回数は増えるので、Aから生えてる(Aの次の)状態に対して、それらすべての遷移に確率を掛けてあげて足してあげる (必ず終了条件を始点として後退解析する)
→「今 = Σ (確率)*(次の期待値 + 1)」
- 後ろから前にいくにつれて回数は増えるので、Aから生えてる(Aの次の)状態に対して、それらすべての遷移に確率を掛けてあげて足してあげる (必ず終了条件を始点として後退解析する)
-
- 期待値は独立であろうがなかろうが、線型性が成り立つ
-
- 状態遷移図を書く。特に、自分に戻ってくる遷移を忘れない!
DP
- 戻すDP → いくつか要素を抜くDPに使える
- 両側からDP → いくつか要素を抜くDPに使える
- 区間DP
- LCS系DP → 文字列系に使える (二次元ナップサックというらしい)
- bit DP
- ダブリング
- In-place DP
- 部分和DP → bitsetで高速化できる
- 桁DP → 1. 普通に桁DP, 2. maspy式の桁DP(1の桁で場合分け → 再帰)
- DPは場合分けの構造である→ 場合分け軸を固定して考えると良い (ARC107 D) →何を軸に場合分けするかを決め打つ (0で場合分けするとか、1の位で場合分けとか)
- 行列累乗
- 巡回セールスマン → 始点はなんでもいいらしい (algo-logic参照)
- 辞書順に復元するなら、後ろからDPをする
- ・メモリを節約しなければならないときのDP → dp $[i\rbrack[j\rbrack[k\rbrack$のiを偶奇に落とし込めば N → 2 に空間計算量が落ちる / 偶奇が入れ替わるとき、INFで初期化 (JOI お菓子の分割)
- 区間DPと両側からDPは違う! → 区間DPはまず最初に幅を決めて, 次に左端を決める(典型019)
- 部分文字列系DP (LCS系DPとは違う) → next $[i\rbrack[j\rbrack$ が肝 O(N)で解ける (ARC 81 E)
文字列
- 置換する問題 → 操作が可逆かどうか / 対称性があるか を見ると良い
- 変換可能か問題 → 返還前後で不変な値は何か? それを用いて、返還前後での値を比べる 「Greedyからの帰着」ってやつ
- 操作後の状態をある程度まとめることができないか実験する (操作後、すでに見たことある状態が存在しないか?
操作系
- 操作を何かしらで特徴づけて、それをdpなりグラフなりで解く
- → ARC 109 D / JOI 20/21 2 /
- 操作の逆元・同値類(もとに戻るやつ)を探す
- 不変量を見る
確率・期待値
- 確率 p で成功する試行を、成功するまで行うときの試行回数(最後の成功した回も含む) の期待値は 1/p
- → ABC 194 D
数列問題
- pos $[l\rbrack$を用意する
- 隣接項の差を取る
- 列の操作は区間DP
- グラフにする
- しゃくとり
ゲーム
- 状態をすべてグラフにすると、後ろから最適なスコアが自ずと導かれる(後退解析) → 自分に不利な手番は放棄していけば、枝刈り的な状態になってdpになる
- Grundy数が何らかの性質から求まらないかを考える
- BostanMoriで $[x^N\rbrack$ P/Q
- スパースな多項式ならmod取らないでもできる(ABC200 E)・負の二項定理
→ 例えば(1-x^n) / (1-x) の形で表されても, ちゃんと割り算できるヨ
クソデカセグ木 → ノードのサイズを恣意的に取れば座圧で対応できる (ARC 115 E)
↓