概要

• pearsonの相関係数は線形な関係しか捉えることが出来ない.
• そこで, 点同士の距離を用いたDistance Correlationという相関係数が提案された.
• さらに, Distance Correlationを拡張し, 内積の期待値が共分散の二乗となるようなヒルベルト空間を定義したPartial Distance Correlationが提案されている. (Székelys, 2014)
  • Partial Distance Correlationを使うと, 条件付けした相関係数 $\mathcal{R}(X|Z, Y|Z)=\mathcal{R}^* (X,Y;Z)$を計算することができる

Distance Correlation

$$a_{k,l} = |X_k-X_l|, \quad \bar{a}_{k, \cdot}=\frac{1}{n}\sum_{l=1}^n a_{k,l}, \quad \bar{a}_{\cdot, l}=\frac{1}{n} \sum_{k=1}^n a_{k,l}, \quad \bar{a}_{\cdot, \cdot} = \frac{1}{n^2} \sum_{k,l=1}^n a_{k,l}, \quad $$

• としたとき

$$A_{k,l} = a_{k,l} - \bar{a}_{k,\cdot} -\bar{a}_{\cdot, l} + \bar{a}_{\cdot, \cdot}$$

• をDistance Matrixと呼ぶ
• このときDistance Matrix $A$を用いて, 以下をDistance Correlationと定義する

$$\mathcal{R}_n^2(x, y) =
\begin{cases}
\begin{array}{cl} \frac{\mathcal{V}_n^2(x, y)}{\sqrt{\mathcal{V}_n^2(x, x)\mathcal{V}_n^2(y, y)}} &, \mathcal{V}_n^2(x, x)\mathcal{V}_n^2(y, y) > 0 \\ 0 &, \mathcal{V}_n^2(x, x)\mathcal{V}_n^2(y, y) = 0 \end{array}
\end{cases}
$$

• ただし, $\mathcal{V}_n^2(x, y) = \frac{1}{n^2} \sum_{k,l=1}^n A_{k,l} B_{k,l}, \quad \mathcal{V}_n^2(x, x) = \frac{1}{n^2} \sum_{k,l=1}^n A_{k,l}^2$

• 分散は一般に平均周りの二次モーメントなので, アナロジー的に平均が0になる必要がある

  • Distance Matrix $A$は要素の行, 列, 全体の平均が0になるので平均周りのモーメントっぽい挙動を振る舞う

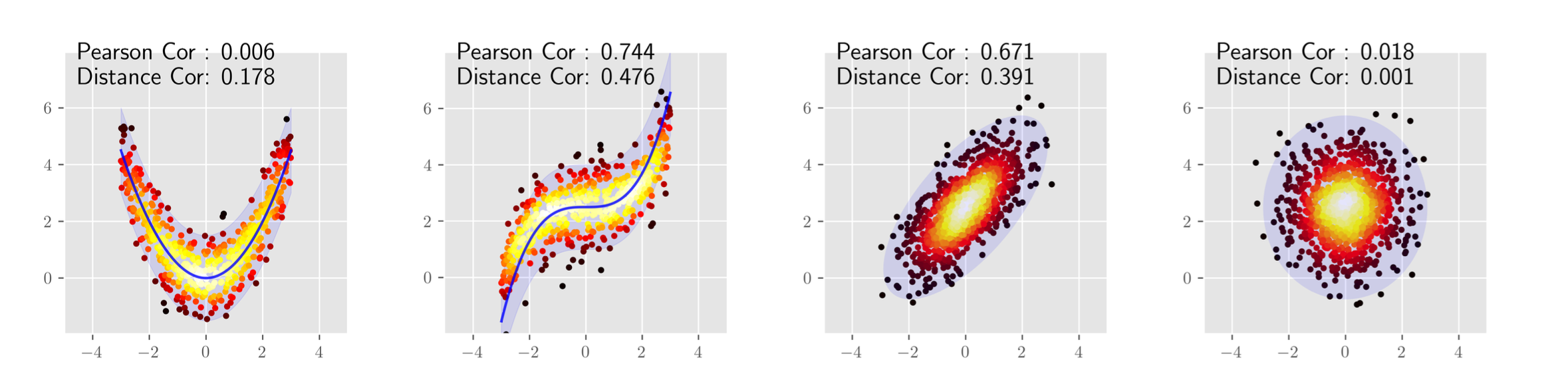
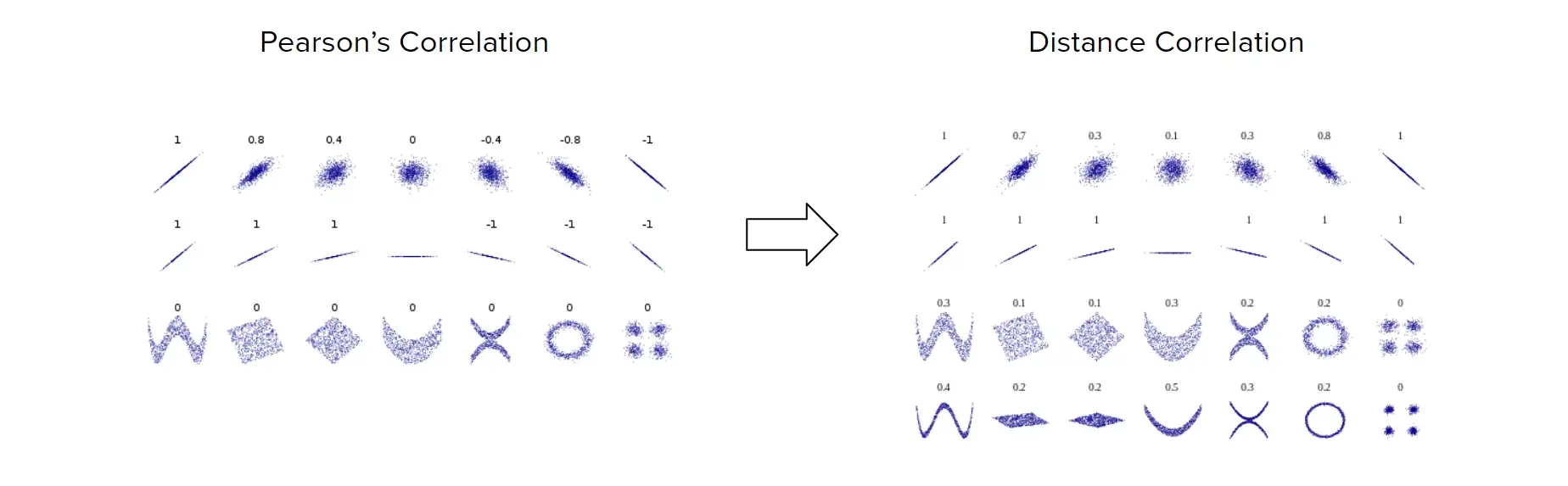
• pearsonは線形な関係しか見ていないのに対して, DCは距離に応じた関係を捉えている. (下図)
  

  

  
  

Distance Correlationと機械学習

• モデルXのある層における出力 $x \in \mathbb{R}^{B\times d_X}$ とモデルYのある層における出力 $x \in \mathbb{R}^{B\times d_Y}$との類似度を計算することができる　
• 注意すべき点として, $x \in \mathbb{R}^{B\times d}$は $d$ 次元の出力が $B$ 個存在する状態なので, Distance Matrix は $B\times B$になることに注意
• 嬉しいことに, Distance Matrix が $B\times B$ になるので, モデルX, Yの出力次元が違っても ( $d_X \neq d_Y$)相関を計算することができる

Partial Distance Correlation の導入

• まず, Distance Matrix $A$を以下のように拡張した $\tilde{A}$を定義する.

$$\tilde{a}_{kl} =
\begin{cases}
\begin{array}{cl}\displaystyle a_{k,l} - \frac{1}{n-2}\sum_{i=1}^n a_{i,l} - \frac{1}{n-2}\sum_{j=1}^n a_{k,j} + \frac{1}{(n-1)(n-2)}\sum_{i,j=1}^n a_{i,j} &, k\neq l\\ 0 &, k=l \end{array}
\end{cases}
$$

• このとき, 内積 $(\tilde{A}\cdot \tilde{B})$を以下のように定義.

$$(\tilde A \cdot \tilde B) := \frac{1}{n(n-3)} \sum_{k\neq l} \tilde A_{k,l} \tilde B_{k,l}$$

• すると, この内積の期待値は $\mathcal{V}^2(x,y)$と一致する (証明は論文参照)
  • 論文ではunbiased estimator of squared population distance covariance (不偏推定量) と呼んでいる

• 上のような $\tilde{A}$を定義すると, 以下の性質が成り立つ. (証明は論文参照)
  1. 要素の行と列の平均がそれぞれ0になる
  2. $\tilde{(\tilde{A})} = \tilde{A}$となる
  3. $\tilde{A}$はdouble centeringに対して不変である

Partial Distance Correlation

• 要は隠れ変数 $z$ が存在するような状態での相関係数を計算したい

  • すなわち, $\mathcal{R}(X|Z, Y|Z)=\mathcal{R}^* (X,Y;Z)$を計算したい

• コイツを計算するには, まずX, YをZに射影したものを用意する必要がある

• 上のような内積が定義されたヒルベルト空間 $\mathcal{H}_n$において, サンプル $x,y,z$におけるDistance Matrix $\tilde{A}, \tilde{B}, \tilde{C} \in \mathcal{H}_n$について
  $$P_{z^{\perp}}(x) = \tilde A - \frac{(\tilde A \cdot \tilde C)}{(\tilde C \cdot \tilde C)}\tilde C, \quad P_{z^{\perp}}(y) = \tilde B - \frac{(\tilde B \cdot \tilde C)}{(\tilde C \cdot \tilde C)}\tilde C $$

• をそれぞれ $\tilde A(x)$を $(\tilde C(z))^{\perp}$に射影したもの, $\tilde B(y)$を $(\tilde C(z))^{\perp}$に射影したものとする.

• すると, ${\mathcal{R}}^2(x,y;z)$ は以下のように定義される. (cosine類似度を相関として使用する感じ？)
  $${\mathcal{R}^*}^2(x,y;z) := \frac{(P_{z^{\perp}}(x) \cdot P_{z^{\perp}}(y))}{|P_{z^{\perp}}(x)| |P_{z^{\perp}}(y)|}$$

• ちなみにpartial distance covarianceは以下のように定義される.
  $$\text{pdCov}(x,y;z)= (P_{z^{\perp}}(x) \cdot P_{z^{\perp}}(y))= \frac{1}{n(n-3)}\sum_{i\neq j} \left(P_{z^{\perp}}(x) \right)_{i,j}\left(P_{z^{\perp}}(y)\right)_{i,j}$$

Partial Distance Correlationと機械学習

• On the Versatile Uses of Partial Distance Correlation in Deep Learning (ECCV22)で提案されているPCDの使いみち
  • $\mathcal{R}^2\left( (X|Y),GT\right)$を計算すると, モデル $Y$を前提としたモデル $X$についてGTとの相関を計算することができる.
  • つまるところ, モデルYが学習した情報を取り除いた状態の $X$とGTの相関を計算することができる
    • どうやって計算するかというと, $X$ を $Y$に射影すれば良い.
    • すなわち, $P_{y^{\perp}}(x) = \tilde X - \frac{(\tilde X \cdot \tilde Y)}{(\tilde Y \cdot \tilde Y)}\tilde Y$を用いて $\mathcal{R}^2\left( (X|Y),GT\right)$を計算する.