はじめに

• CVPR22
• 決定境界を描画し, 再現性と汎化性について定量的に考察した論文

決定境界の描画 (領域の決定)

• 如何に決定境界を描画するかが重要になってくる

  • その上でまず, データ多様体 $\mathcal{M}$の近傍(on-manifold)を取るのか, $\mathcal{M}$から離れた領域(off-manifold)を取るのかを考える必要がある

  • 結論からいえば, データ多様体 $\mathcal{M}$付近の挙動を調べるほうが良い

    • 決定境界はほぼデータ多様体近傍に存在することが実験的・理論的にわかっている
    • 実際に著者らは, 以下の補題を証明している
      • $f:[0,1\rbrack^n \to [0,1\rbrack$であって $|f(x) - f(y)| \le \frac{L}{\sqrt{n}}|x-y|$を満たすようなNNに関して, $\bar{f}$を単位超立方体における $f$の値の中央値だとすると, 画像 $x$が $|f(x) - \bar{f}| \le t$を満たす確率は
        $$ 1-\frac{Le^{-2\pi n t^2/L^2} }{\pi t \sqrt{n} } $$
      • すなわち, NNがリプシッツ連続でさえあれば, 出力はほとんど中央値の近くに存在する (expの中が負なので)

  • Off-manifold → ❌
    

    

    
    

  • On-manifold → ⭕

決定境界の描画 (描画方法)

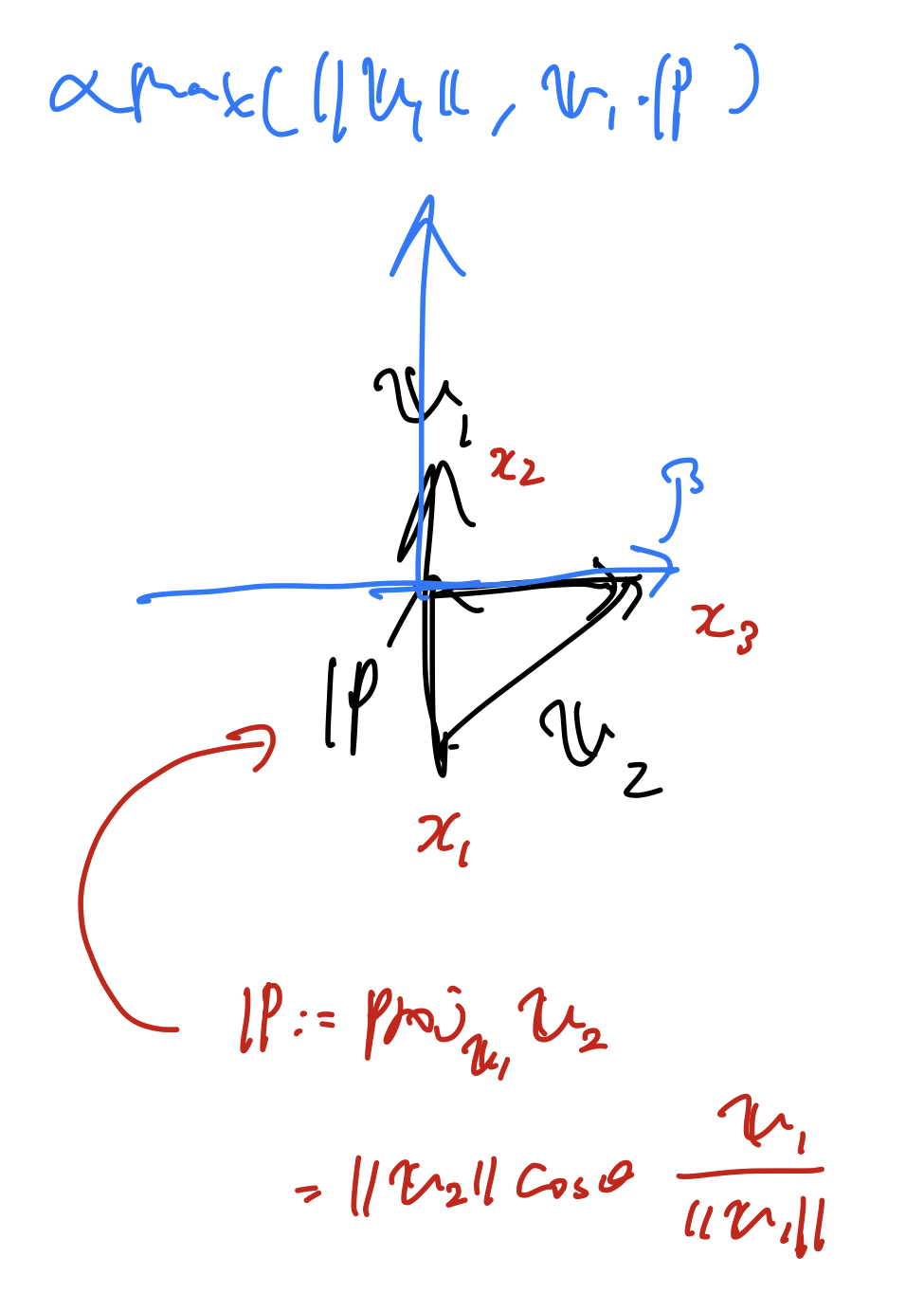
• 決定境界がデータ点の凸包においても構造化されているという仮定のもと, 以下のように描画する.

  • (なぜここで凸包が持ち出されたのかがよくわからない…)
  • (論文ではMixupの論文の方法に則っているというが, そもそも論文中に当該箇所が見つからなかった…)

• まずは $(x_1,x_2,x_3)$点を適当にサンプリング

• $\vec{v_1} = x_2-x_1, \vec{v_2} = x_3-x_1$として, 下式において $\alpha, \beta$を $-0.1 \leq \alpha, \beta \leq 1.1$の間で動かす.

$$\alpha \cdot \max(\vec{v_1} \cdot \vec{v_1}, |\text{proj}_{\vec{v_1}}\vec{v_2} \cdot \vec{v_1}|)\vec{v_1} + \beta (\vec{v_2} - \text{proj}_{\vec{v_1}}\vec{v_2})$$

実験

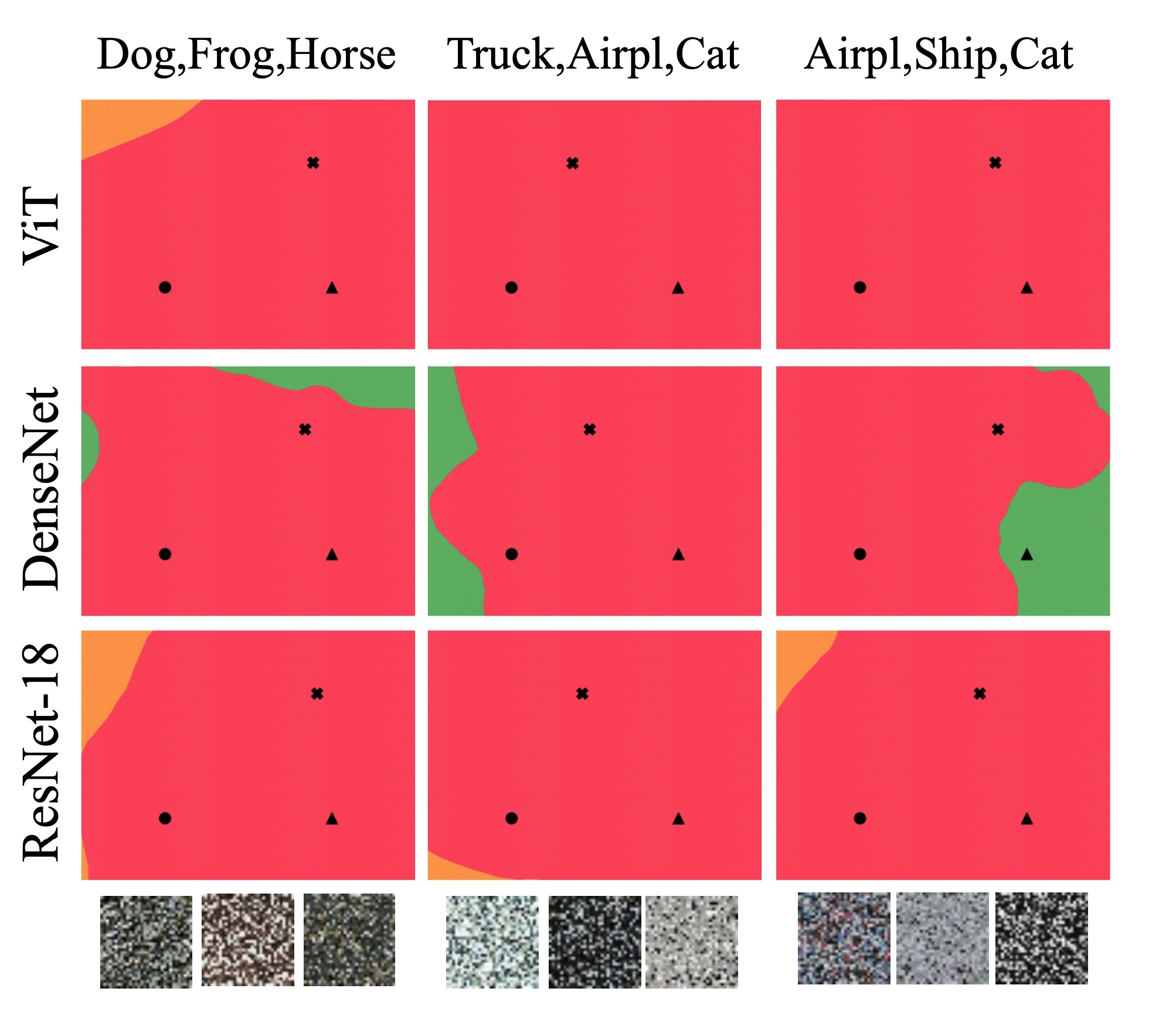
結果1 : 帰納バイアスによる違い

• 結果1 : 帰納バイアスによる違い
  • CNN系は決定境界が似ている
  • 一方で, ViT, MLP-Mixer, FCもやや似ている
  • 特にCNN系ではオレンジ(label=AUTO)が全く出てこないのに対して, 前３つでは出現している
    • CNN系はのっぺりしており, 再現性が期待される

結果2 : 定量的比較

• 結果2 : 定量的比較
  • モデルのパラメタ $\theta_1, \theta_2$についてRegion Similarity Scoreを定義　
    $$R(\theta_1, \theta_2) = \mathbb{E}_{T_i \sim \mathcal{D}} \bigg[(|f(S_i, \theta_1) \cap f(S_i, \theta_2)|) / |S_i|\bigg\rbrack$$
  • ただし, $f(S_i, \theta) = {(x,f(x;\theta))}_{x\in S_i}$
  • つまり, 適当な格子点 $x$に対して, その点 $x$の出力 $f_\theta (x)$が同じクラスである確率
  • で, それらを比較した結果が下の図

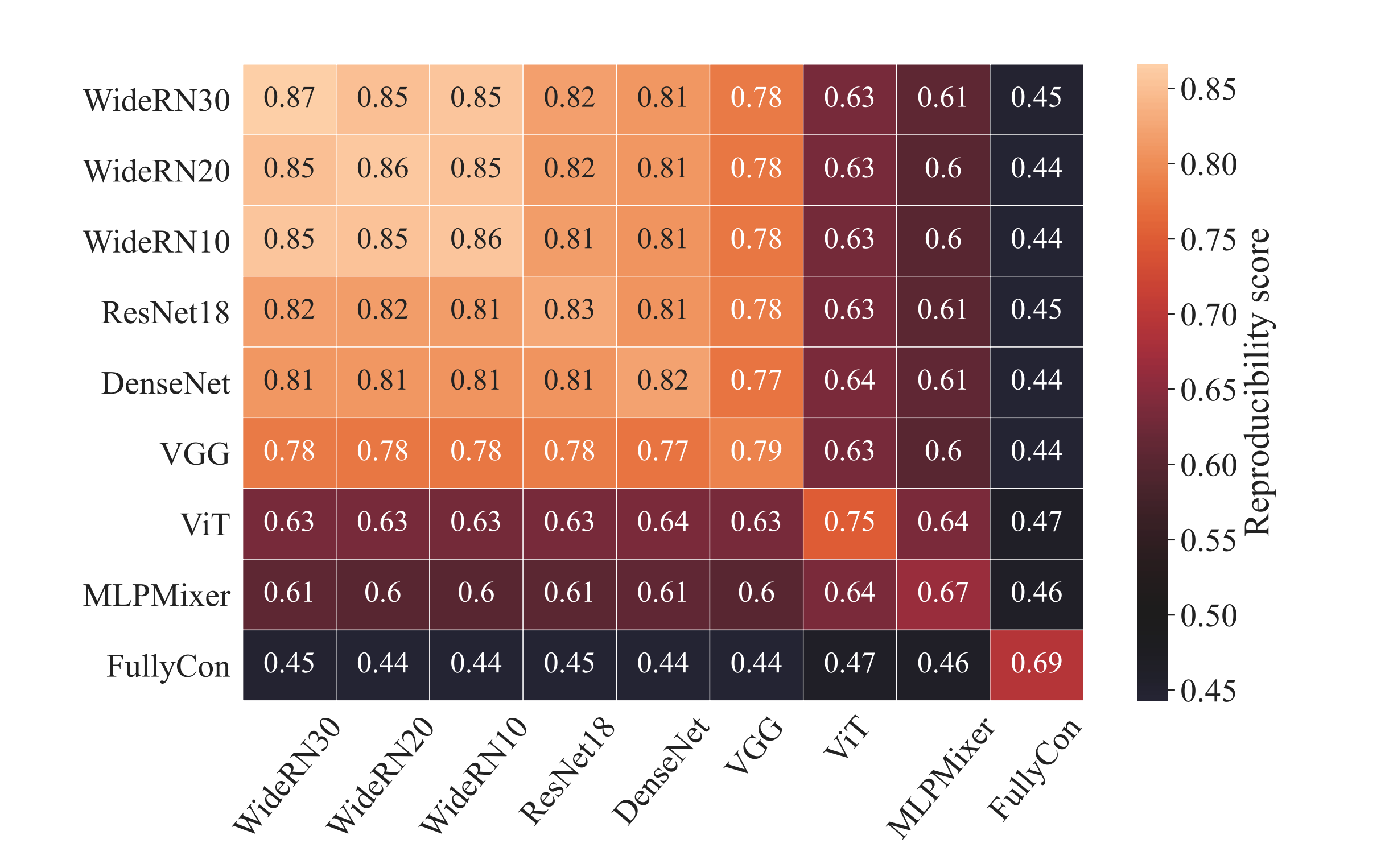
• 上図からわかったのが以下の三点
  1. 畳み込みの帰納バイアスを持つモデルは似た決定境界を持つ一方, MLP-MixerやViTなどは互いに異なった領域を描く
  2. CNNの幅が大きければ大きいほど再現性が高くなる
  3. 残差接続は決定境界にあまり影響しない

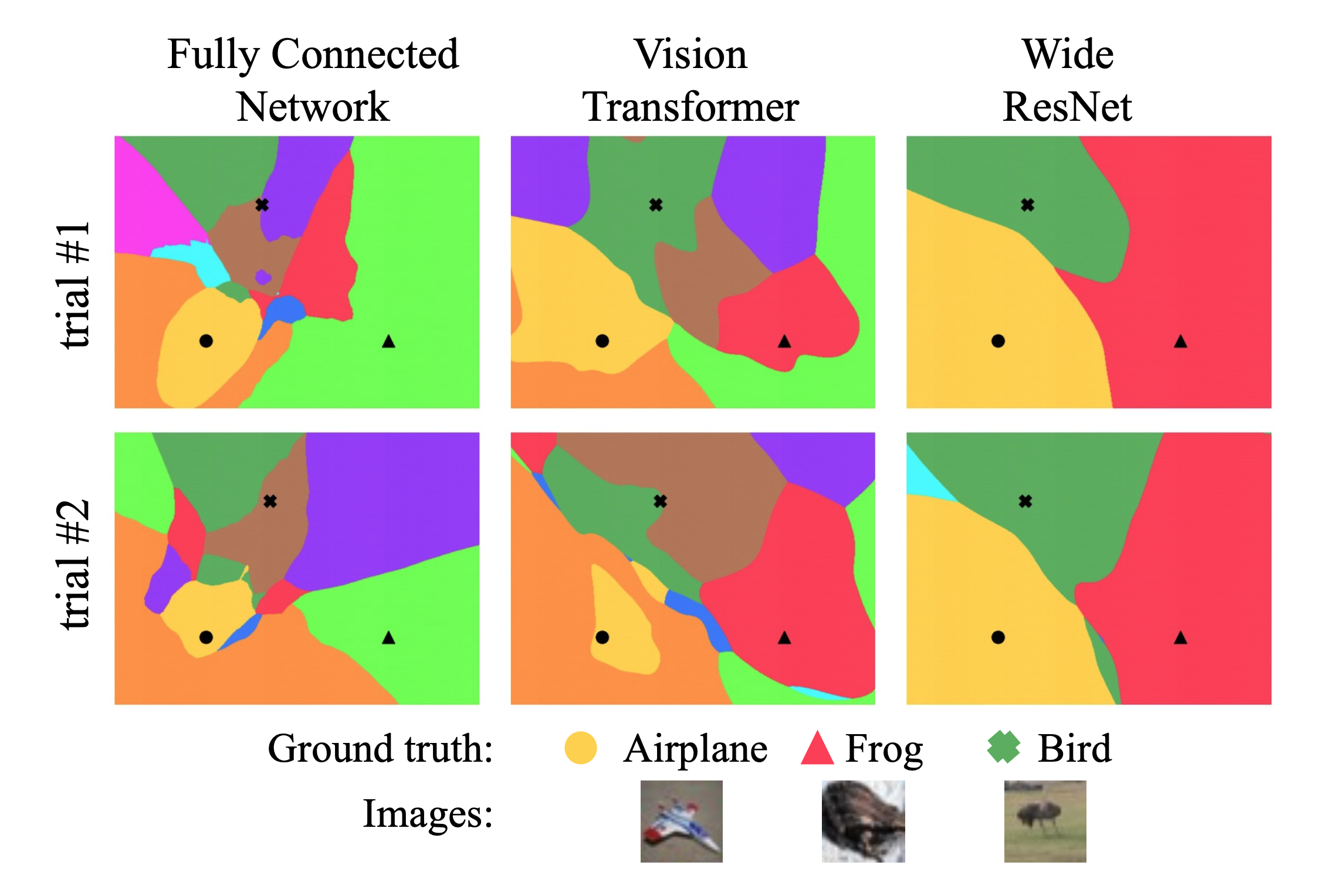
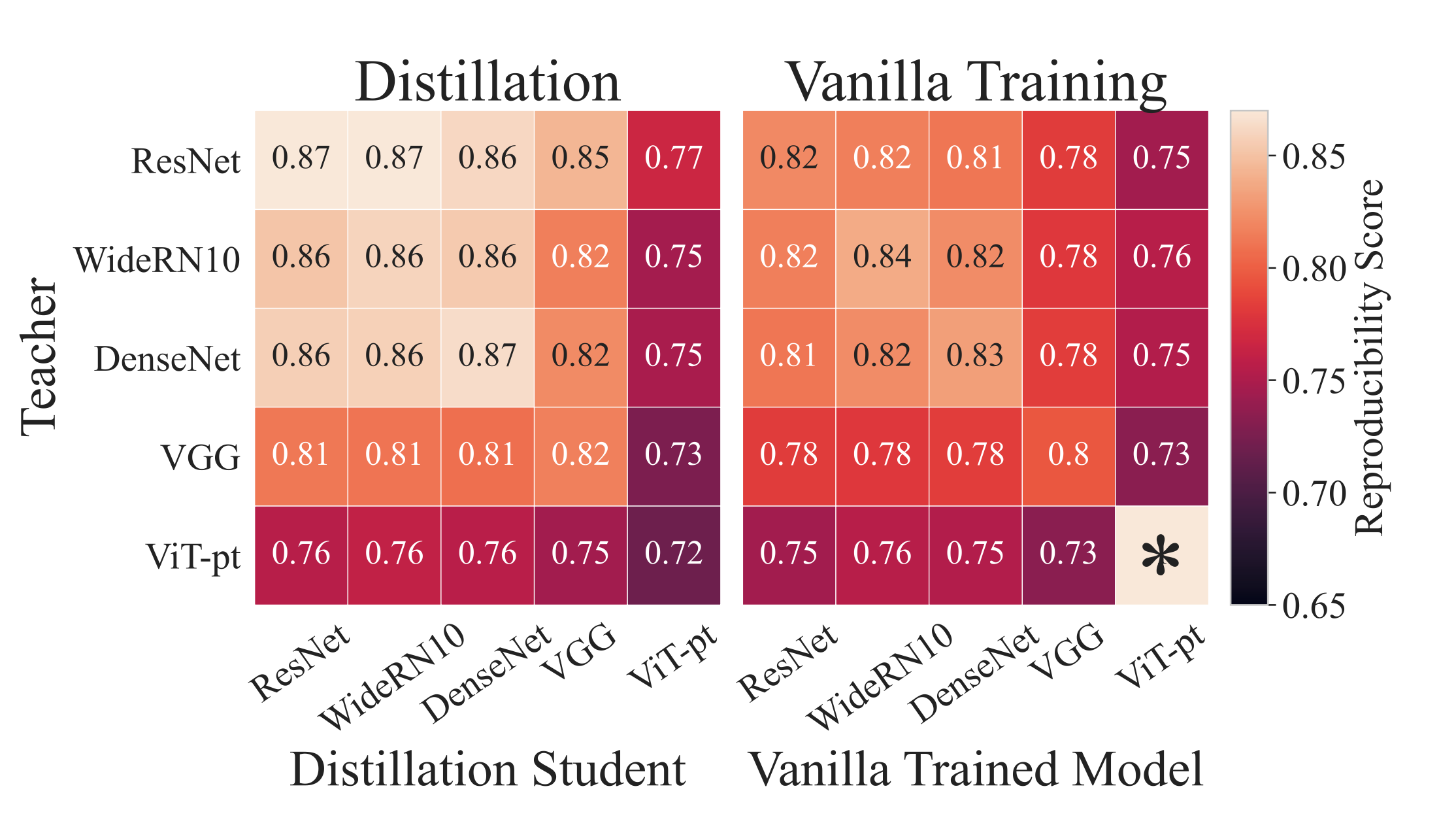
結果3 : 蒸留は決定境界を歪めるか？

• 結果3 : 蒸留は決定境界を歪めるか？
  • 今まで双方の意見が出されていたらしいけど, 結論はNO
  • ほとんどのモデルで, 似たような決定境界を得ることができる

結果4. Double Descentについて

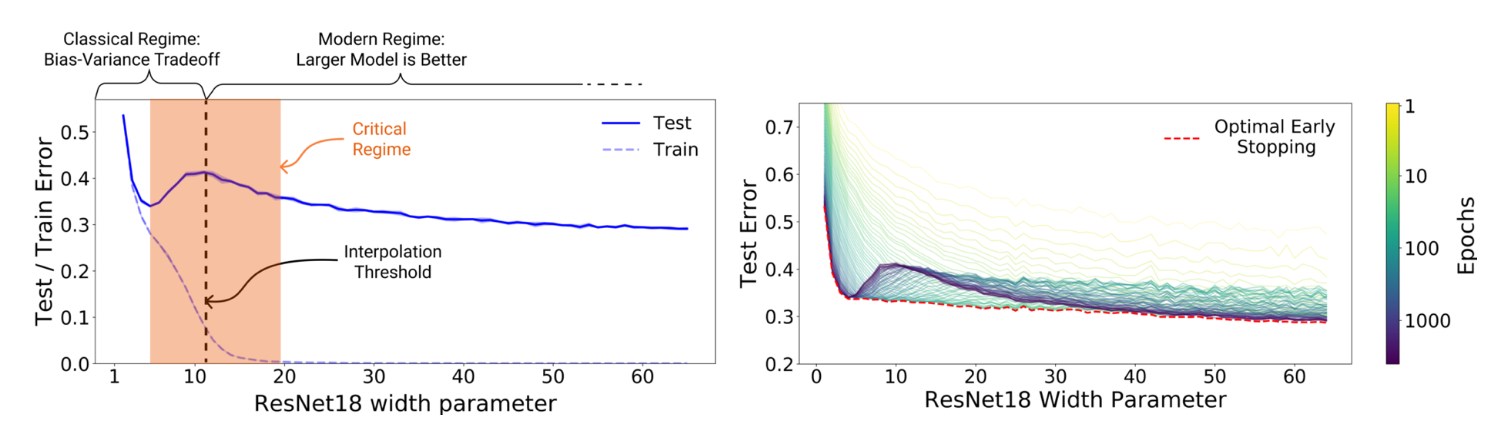
• 結果4. Double Descentについて
  • Double Descent: NNに特有の現象で, パラメタを複雑にしていくと, lossが二回減少する現象
    • (下図: U字カーブになっている)
    • (補足: 近年のモデルではbias-variance分解は破綻しており, 古典的な議論とされている. 現在ではモデルの複雑度を上げるとどちらも減少することが経験的に知られており, Double Descentの文脈では頻出の議論である.)

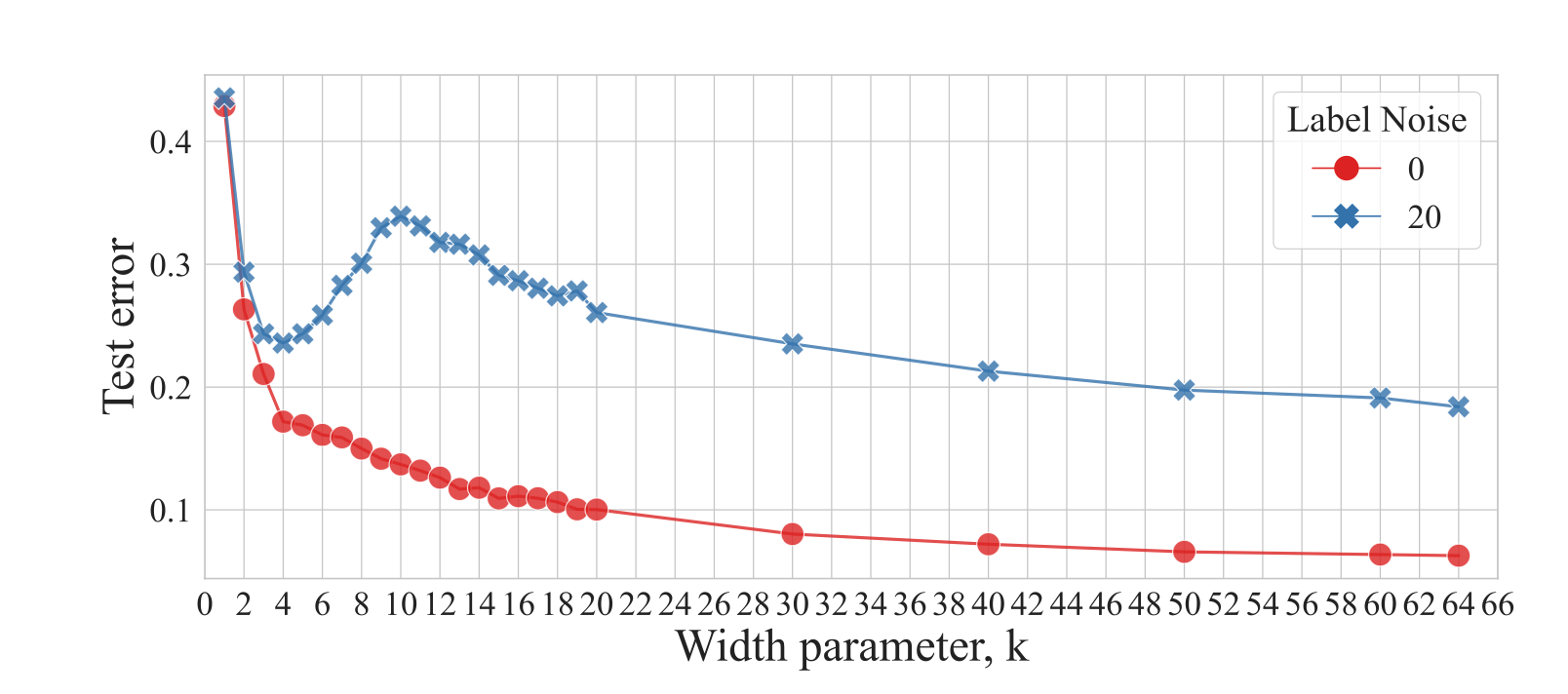
• Double Descentはラベルノイズが含まれている場合に容易に再現できることが知られている

• なので, 今回は20%のラベルノイズが入ったデータセットを実験に用いる

• 実験設定: ResNetのカーネルサイズ $k$を変動させる

  • $k$を変化させたときのlossの変動が下図
  • 大体 $k = 10$くらいが閾値となって, lossが再降下している

• 実際に決定境界を描画すると下のような感じ
  • $k = 7, 10$あたりから領域の断片化が発生しており, $k$が十分に大きくなると断片化は収まる
  • これらから, 領域がどれだけ断片化(fragmentation)されているかが重要そうなことがわかる

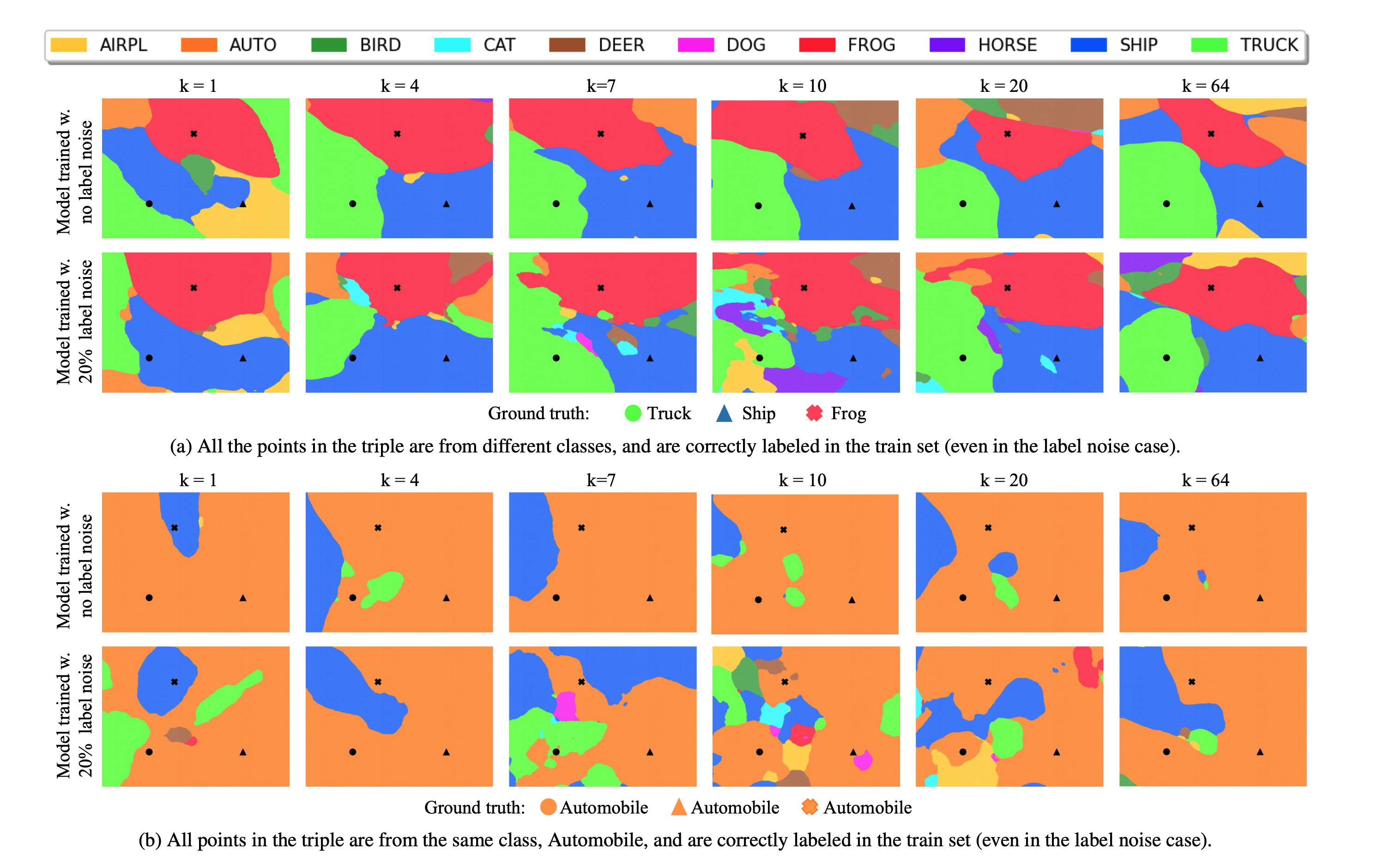
• ラベルの誤ったサンプルについて, 決定境界を描画するとこんな感じ
  • 当該サンプルは $\times$で描画されている
    • 例えば, 左上の $\times$は本来automobileだがbirdとラベリングされたサンプル
  • $k=10$だと境界付近にサンプルが存在することが多い
  • 一方で $k=64$と十分にモデルが複雑な場合, 帰納バイアスによって孤島が出来上がっている

• ということで, Double Descentはfragmentationの増加が一要因となっていると思われる