はじめに
- NeurIPS22
- Few-shotにおける knowledge graph completion task を行う
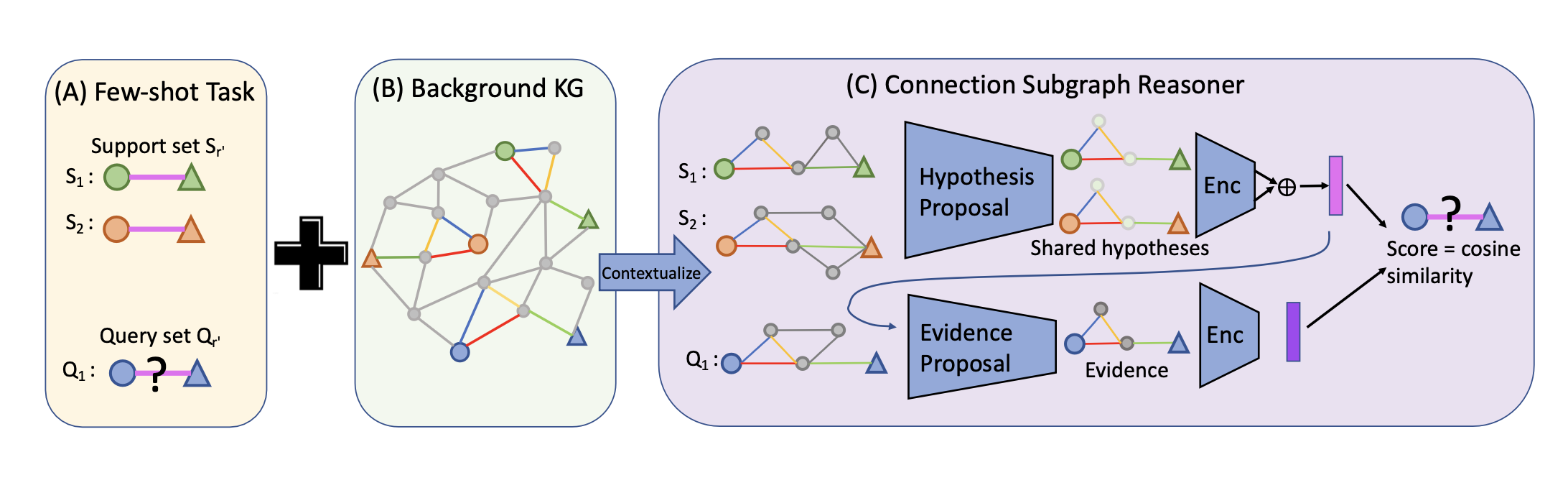
- 上図のように, Background KG (knowledge graph)とsupport setが与えられた状態で, Query setのrelationを推論するタスク
- Connection Subgraph Reasoner (CSR)を提案
- Few-shotにおける knowledge graph completion task を行う
Few-shot KG Completion
-
KGは $\mathcal{G} = (\mathcal{E}, \mathcal{R}, \mathcal{T}) $で表される
- ここで, $\mathcal{E}, \mathcal{R}$はそれぞれentityとrelationで, $\mathcal{T}$はtripletで $\mathcal{T} = { (h, r, t) | h, t \in \mathcal{E}, r \in \mathcal{R} }$
-
Few-shotknowledge graph completion taskとは
- $r’ \not \in \mathcal{R}$なような $r’$について (=unseenなrelationについて)
- support set $S_{r’} = {(h_k, r’, t_k) | h_k \in \mathcal{E}}_{k=1}^K$が与えられた状態で
- $Q_{r’} = {(h_j, r’, ?) | h_j \in \mathcal{E}}_{j=1}^J $の"?“に該当するentityを当てるタスク

引用: M. Chen, W. Zhang, W. Zhang, Q. Chen, and H. Chen. Meta relational learning for few-shot link prediction in knowledge graphs. In EMNLP, 2019.
Inductive Reasoning
-
以下のようなものをhypothesisと呼ぶ
$$\exists Z, (h_c,\text{can be done with},{Z}) \land ({Z},\text{is located at},{t_c}) \implies ({h_c},{\bowtie},{t_c}).$$ -
基本的には有効なhypothesisを探すことを目的とする
General Framework
- まずは一般化されたフレームワークを提案している
- このフレームワークに則り,Learning-freeな方法(CSR-OPT)と学習可能な方法(CSR-GNN)の二つを提案している
- Triplet Contextualization
- support setとクエリのTripletに対して, background KGからサブグラフを作成する
- 具体的には, ノードからk-hopで到達しうるノードまでを使ってサブグラフを構成する
- これにより知識グラフによって"contextualized"されたグラフを得ることができる
- Hypothesis Proposal
- 一般にhypothesis proposal module と呼ばれる $M_p$を用いて, support setに対する全てのサブグラフに対してhypothesisを提案する
- $M_p$はどのエッジを採用するかを示すsoft edge mask $m: [0,1\rbrack^{E}$を出力する
- エッジを採用 = tripletを採用
$$\begin{align}
{m_i}_{i= 1}^K &= M_{p}({G(h_i, t_i) | (h_i, r’, t_i) \in S_{r’}}) \\
b &= \frac{1}{K} \sum_{i= 1}^K M_{enc}(G(h_i, t_i), m_i) \\
\end{align}$$
- ただし, $M_p$は以下の式を満たす必要がある ( $s$はcosine類似度)
$$\begin{align}
\arg\max(\sum_{i= 1}^K \sum_{E} m_i),
s.t. \forall i,j \in 1…K, \\
s(M_{enc}(G(h_i, t_i) , m_i) , M_{enc}(G(h_j, t_j) , m_j)) > 1- \epsilon \end{align} $$
- Hypothesis Testing.
-
一般にevidence proposal module $M_e$と呼ばれる $M_e$を用いてhypothesisが正しいかどうかを検証する
$$\begin{align}
m_q &= M_{e}(b, G(h_q, t_q)) \\
score &= s(b, M_{enc}(G(h_q, t_q), m_q)) \\
\end{align}$$ -
ただし $M_e$は以下の式を満たす必要がある ( $s$はcosine類似度)
$$s(M_{enc}(G(h_q, t_q) , m_q), b) > 1- \epsilon$$
CSR-OPT (Learning-free)
-
hypothesis proposal module $M_p$について, 以下の最適化問題を解く
$$M_{p}({G(h_i, t_i) | (h_i, r’, t_i) \in S_{r’}}) = \arg\max \sum({m_i}_{i= 1}^K) - \lambda * H(m_q)$$
$$\begin{align}
s.t. \sum s(M_{enc}(G(h_i, t_i), m_i), M_{enc}(G(h_j, t_j), m_j)) &> 1- \epsilon’, \\
\texttt{connectivity}(m_i) &> 1- \epsilon’ \\
\end{align}$$- ただし, $\texttt{connectivity}$は $A$を隣接行列, $R_{i,j} = min((I + A + A^2)[i,j\rbrack, 1)$として, 以下の通り
$$\texttt{connectivity}(m_i) =\frac{1}{|E|} \sum_{e = (n,n’)\in E} m_{ie} * \min(R_{n,h_i} +R_{n,t_i}+R_{n’,h_i}+R_{n’,h_i}, 1) $$ - おそらく $k\texttt{-hop}, k \in [0,2\rbrack$なので $A^2$とか出てくる
- ただし, $\texttt{connectivity}$は $A$を隣接行列, $R_{i,j} = min((I + A + A^2)[i,j\rbrack, 1)$として, 以下の通り
Aが無向または有向グラフGの隣接行列とすると、行列An(すなわちAのn個の複製の積)は興味深い解釈を持つ: 要素(i, j)は頂点iから頂点jへの長さnの(有向または無向)歩道の数を与える。nが、あるi、jについてAnの要素(i, j)が正となるような最小の非負整数とすると、nは頂点iと頂点jとの間の距離である。
引用: Wikipedia ─ 隣接行列
-
evidence proposal module $M_e$について, 以下の最適化問題を解く ( $H(\cdot)$は正則化項)
$$T(b, G(h_q, t_q)) = \arg\max s(b, M_{enc}(G(h_q, t_q), m_q)) - \lambda * H(m_q)$$- $M_{enc}$はランダムなGNN (要検証)
CSR-GNN
- $f_{enc}(G_1, m_1): \mathcal{G} \times \mathbb{R}^{|\mathcal{E}|} \to \mathbb{R}^d$, $f_{dec}(G_2, b): \mathcal{G} \times \mathbb{R}^d \to \mathbb{R}^{|\mathcal{E}|}$として, それぞれを $M_p$, $M_e$とする
- $f_{dec}$にはPathConを使用
- Relational Message Passing for Knowledge Graph Completion (KDD21)


- 学習方法
-
reconstruction loss とcontrastive lossを使用
$$\begin{align}
Loss_{recon} &= \ell_{\text{CE}}(m, f_{dec}(G, f_{enc}(G, m))) \\
Loss_{contrast} &= \max( s(g_{pos}, g) - s(g_{neg}, g) + \gamma, 0)\\
\end{align}$$ -
$g$に関して,
-
同じrelationに対して異なるtripetをサンプリングしてきたものを $G, G’$として正例と負例を作る
-
$$\begin{align}
g &= M_{enc}(G, m) \\
g_{pos} &= M_{enc}(G, f_{dec}(G, f_{enc}(G, m))) \\
g_{neg} &= M_{enc}(G’,f_{dec}{G’, f_{enc}(G, m)})
\end{align}$$
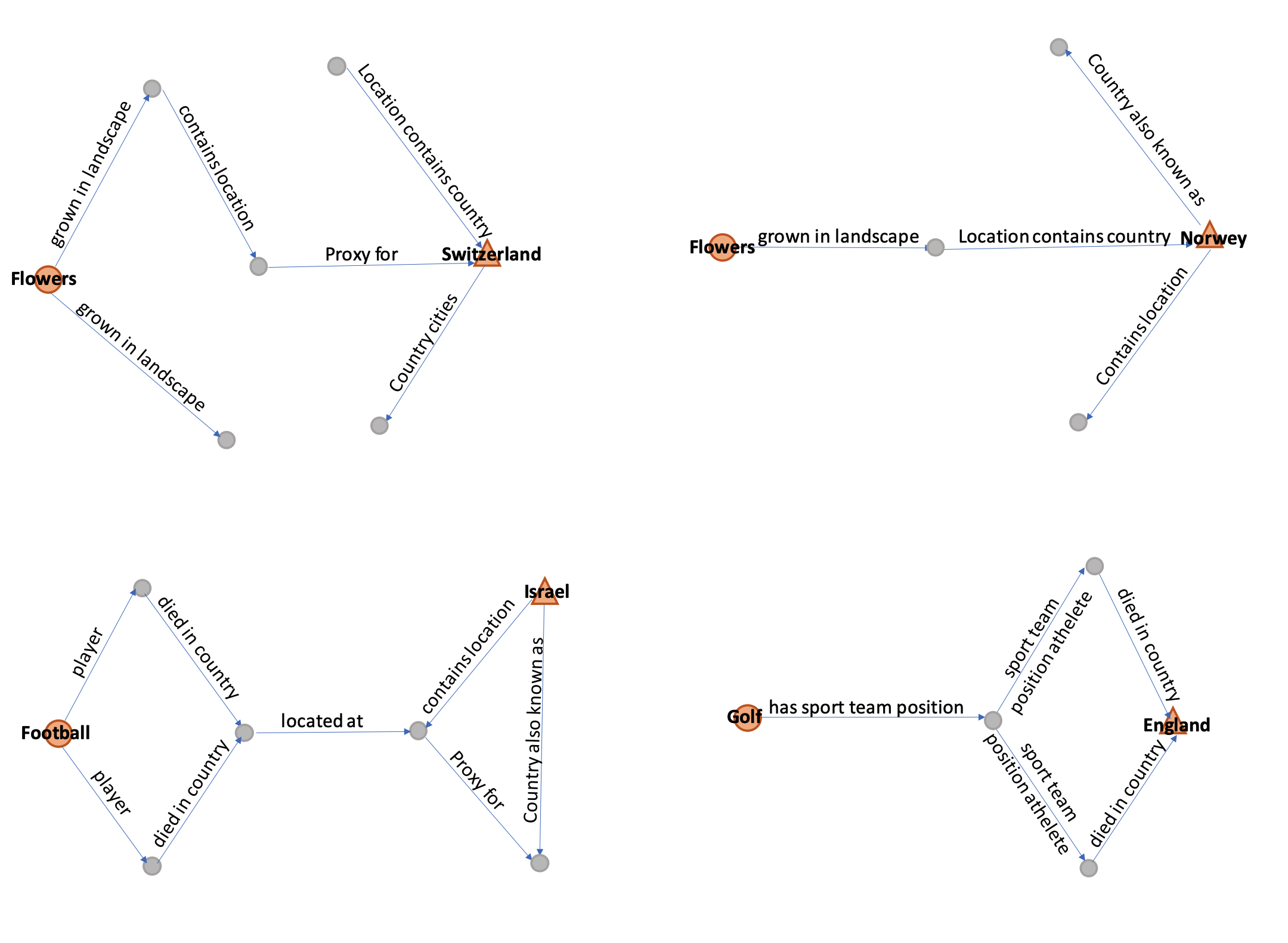
実際の推論例