【論文メモ】Perceiver: General Perception with Iterative Attention

JavaScriptを有効にしてください

【論文メモ】Perceiver: General Perception with Iterative Attention

📅 2022/7/11 · ☕ 1 min read

#論文

Transformer を改善
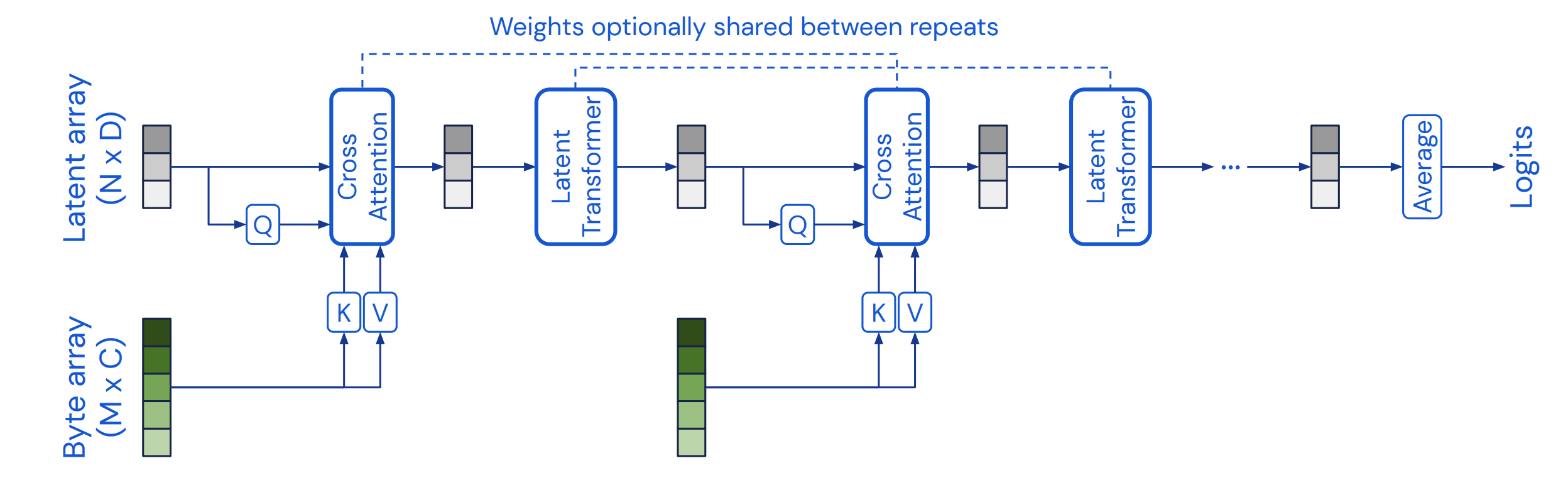
- Qを潜在変数とすることで, $L^2$の呪いから解放してあげる
- 音声系 / 時系列予測にも適してる
潜在変数をcentroidとして, 高次元の入力 $x$ をend-to-endでクラスタリングしてるとも捉えうる
- つまり, 入力 $x$をタグ付けしてるイメージ (と論文内で言っている)
Positional Encoding
- 普通のPEの代わりに, フーリエ変換した特徴量を使う

1
2
3
4
5


    scales = torch.linspace(1., max_freq / 2, num_bands, device = device, dtype = dtype)
    scales = scales[(*((None,) * (len(x.shape) - 1)), Ellipsis)]
    x = x * scales * pi
    x = torch.cat([x.sin(), x.cos()], dim = -1)
    x = torch.cat((x, orig_x), dim = -1)

https://github.com/lucidrains/perceiver-pytorch/blob/main/perceiver_pytorch/perceiver_pytorch.py#L33
NeRFと関連が深いらしい
- Rahamanによると, NNは低周波数を学習しがちらしい (ON THE SPECTRAL BIAS OF NEURAL NETWORKS (ICML18))
- なので, 事前に入力を高周波成分を用いた高次元空間に飛ばせば, 高周波なものも学習しやすくなるらしい (by NeRF)

We use a parameterization of Fourier features that allows us to (i) directly represent the position structure of the input data (preserving 1D temporal or 2D spatial structure for audio or images, respectively, or 3D spatiotemporal structure for videos), (ii) control the number of frequency bands in our position encoding independently of the cutoff frequency, and (iii) uniformly sample all frequencies up to a target resolution. We parametrize the frequency encoding to take the values (sin(fkπxd), cos(fkπxd)), where the frequency fk is the k th band of a bank of frequencies spaced equally between 1 and µ 2 . µ 2 can be naturally interpreted as the Nyquist frequency (Nyquist, 1928) corresponding to a target sampling rate of µ.

追記
- Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains を読むと良い
- https://github.com/lucidrains/perceiver-pytorch/blob/main/perceiver_pytorch/perceiver_pytorch.py#L227

著者

YuWd (Yuiga Wada)

機械学習・競プロ・iOS・Web

【論文メモ】Perceiver: General Perception with Iterative Attention

関連記事